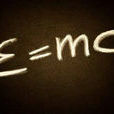質能轉換公式

質能轉換公式是一種闡述能量（E）與質量（m）間相互關係的理論物理學公式，公式中的c是物理學中代表光速的常數。

基本介紹

• 中文名：質能轉換公式
• 發現人：愛因斯坦
• 基本公式：E=mc2

方程式意義

該公式表明物體相對於一個參照系靜止時仍然有能量，這是違反牛頓系統的，因為在牛頓系統中，靜止物體是沒有能量的。這就是為什麼物體的質量被稱為靜止質量。公式中的E可以看成是物體總能量，它與物體總質量（該質量包括靜止質量和運動所帶來的質量）成正比，只有當物體靜止時，它才與物體的（靜止）質量（牛頓系統中的'質量'）成正比。這也表明物體的總質量和靜止質量不同。

反過來講，一束光子在真空中傳播，其靜止質量是0，但由於它們有運動能量，因此它們也有質量。

術語的不同

注意：有些術語使用中，質量單指靜止質量，因為總質量和能量是等價的概念。若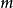 指代靜止質量，則公式應改寫為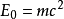

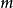
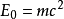
而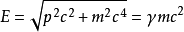

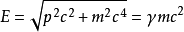
因此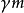， 也就是總質量的表達式，其中 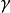為洛倫茲因子。

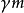
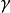
方程的證明

以一外力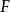 對物體作功，根據功-動能定理，物體的微小動能變化為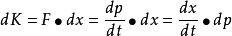

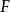
式中， 為物體的動量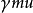 (此處的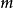 為靜止質量)，而 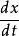為物體的速度 。因此此式可改寫為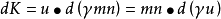

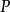
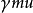
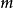
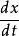
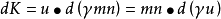
根據以下等式(詳見四維速度)，

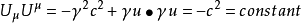
將等式的兩側取微小量並重新整理，

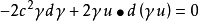
u

以此等式代入上方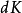 的關係式得

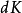
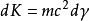
此即為相對論下的動能表達式，注意式中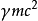 僅與四維動量的時間分量相差一比例常數 。若以此定義物體的能量，

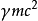
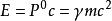
則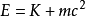 其中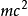 為物體因具有質量而具有的能量，即

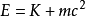
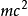
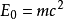
註：若改以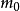 表示內秉質量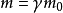， 表示相對論質量，則亦有之關係。

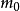
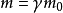
可套用性

適用於所有有質量的物體，因為它是質量由能量導出的斷言，或者說能量由質量導出的論斷，而兩者可以互相取代。它對運動物體的套用依賴於方程中使用的質量的定義。

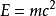
通常，該方程用於相對於物體不動的參考點。但是同樣的物體從另外一個參照系來看可以是運動的，所以，對於這個參照系，該方程表示質量是不同的。

從現代物理的觀點來看，這個方程表示物質和能量是同一個概念。

愛因斯坦和他的1905年論文

阿爾伯特·愛因斯坦沒有在他的1905年論文中精確地表述這個方程"Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?"（“一個物體的慣性依賴於它所包含的能量嗎?”，發表於《物理學年鑑》9月27日），這是他現在被稱為《奇蹟年論文》的文章之一。

該論文所說的確切內容是：‘若一個物體以輻射形式發射能量L，它的質量減少L/c²。’，這個情況下輻射的是動能，而質量是那時候通常所指的質量，也就是今天我們根據情況稱為靜能量或者不變質量。這是在發射能量前後的質量差，它等於L/c²，而不是物體的整個質量。在那時它僅僅是理論上的還未被實驗證明。

其他貢獻

愛因斯坦不是唯一將能量聯繫到質量的人，但他是第一個將這個作為更大的理論的一部分推出的，而且，是根據這個理論的前提所導出的結果。

根據Umberto Bartocci（佩魯賈大學數學史家），該方程早在兩年之前就由Olinto De Pretto發表了，他是一個義大利維琴查的工業家。但是沒有主流史學家認為這個結論是真實的或者是重要的，他們認為即便De Pretto是首位發現該公式的人，但是只有在愛因斯坦真正將它和相對論建立聯繫之後，該公式才真正顯示出價值。