在利用場論計算有相互作用的粒子散射、衰變的過程時,需要逐階微擾展開計算。常用的一種展開方法可以用圖形化的語言進行表述,這就是費曼圖。而費曼圖與具體計算時所使用的算式之間的關係就是費曼規則。
基本介紹
- 中文名:費曼規則
- 外文名:Feynman Rules
- 領域:量子場論
定義,QED的費曼規則,套用,
定義
一般在計算有相互作用粒子散射、衰變的過程時,會將相互作用項看成微擾部分進行展開,為了方便寫出每階微擾的所有項而不重複或漏項,費曼提出了一種圖形化來表達的方法,每一個費曼圖代表一項。而費曼圖中包含:外腿、頂點、傳播子等部分,每一部分對應不同的數學表達式。圖形與表達式之間的對應規則被稱為費曼規則。
一般而言外腿、頂點、傳播子對應相應的算式,按照費米子線相反的方向逐項寫出,再對不確定動量進行積分、求跡(trace)運算,再乘上圈圖提供的因子和對稱因子就可以得到對應的費曼振幅。
QED的費曼規則
傳播子部分如圖1:
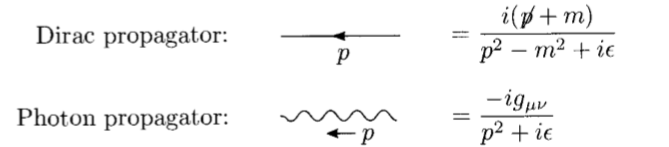 圖1
圖1頂點部分如圖2:
 圖2
圖2外腿部分如圖3:
 圖3
圖3套用
費曼規則在當今量子場論中是不可或缺的重要概念。費曼將圖形化的語言引入到物理學具體的計算中也是理論物理界開創性的工作。
在高能物理、粒子物理中,一般使用相對論性的場論,其費曼規則一般也就比較方便寫成具有洛侖茲結構的普遍表達式。
在凝聚態物理中,一般使用非相對論性的場論,費曼規則往往對應著格林函式。而因為凝聚態方向相互作用項限制較小,具體問題不同也不一樣,所以格林函式的具體形式往往也不一致。

