變形分配法

變形分配法，位移法的一種，通過廣義位移（線位移和角位移）的疊代過程求解連續梁和剛架一類靜不定結構的位移和內力的方法，又稱變形傳播法，是捷克所洛伐克的C. V. 克盧切克於1938年首先提出的。

基本介紹

• 中文名：變形分配法
• 外文名：deformation distribution method
• 提出者：C. V. 克盧切克
• 提出時間：1938年

要點

變形分配法的要點如下：

考慮到連續梁和無側移剛架的位移法方程組中每個方程最多含有三個未知廣義位移，且首尾兩方程只含兩個未知廣義位移，其形式為：

K₁₁x₁+K₁₂x₁+R₁=0

K₂₁x₁+K₂₂x₂+K₂₃x₃+R₂=0

K₃₂x₂+K₃₃x₃+K₃₄x₄+R₃=0

……

K_n-1,n-2x_n-2+K_n-1,n-1x₃+K_n-1,nx₄+R_n-1=0

K_n,n-1x_n-1+K_n,nx_n+R_n=0，

式中K_i,j為已知的剛度係數，且K_i,j=K_j,i，R_i為結構中節點i處由外載荷引起的相應約束上的反力（或固端力矩）；x_i為節點的未知廣義位移。對於此類方程，可以方便地用疊代法求解。首先，在第一個方程中假設R_i=0，並令

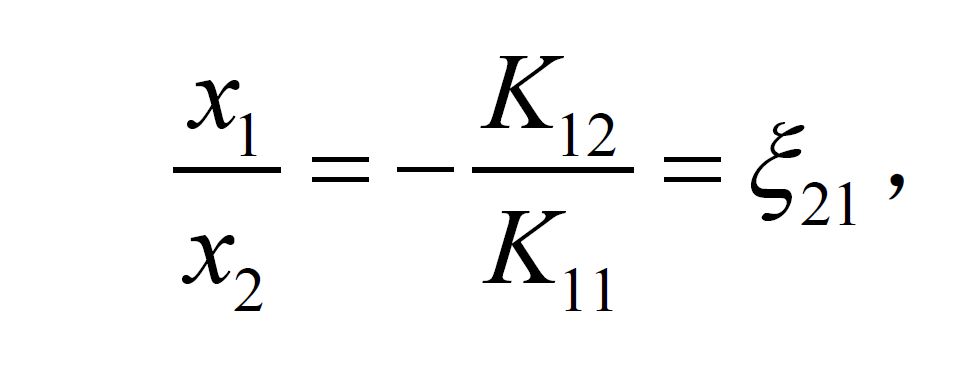
公式

它是節點2對於節點1的位移傳播係數。將

變形分配法

代入第二個方程，便得一個只含兩個未知量的方程。再假設R₂=0，重複以上的過程，可得：

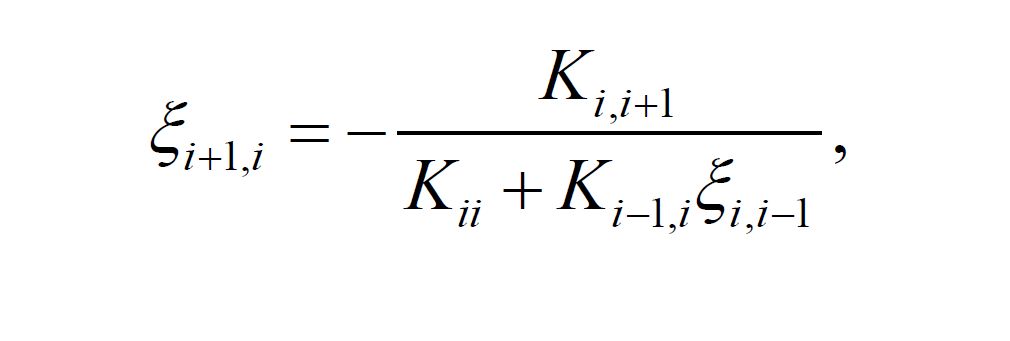
公式

為節點i+1對節點i的位移傳播係數，若已知一個

公式

均可求出。在此基礎上，令第m個方程的自

公式

由項R_m不為零，而其餘各方程的自由項均為零，可得節點m的位移，即

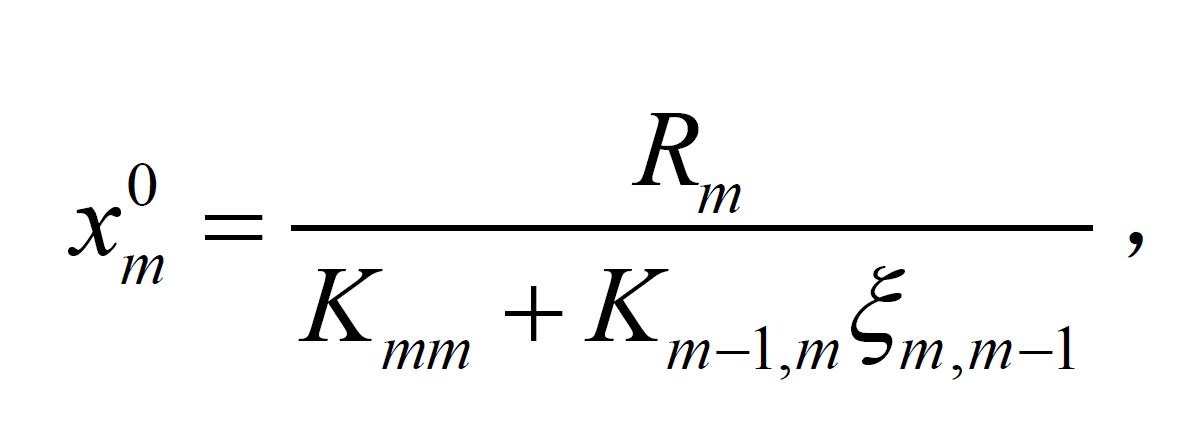
公式

利用位移傳播係數，就可算出其他點因R_m的存在而產生的位移。分別計算出各自由項的影響，再經疊加，就可得到各廣義位移的最終結果，並可進而求出結構中的內力。