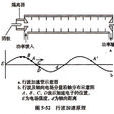
簡介,入射行波與反射行波,性質,行波測距式距離保護原理,行波測距式距離保護的基本原理,行波測距式距離保護的動作特性分析,行波測距式距離保護存在的主要問題,方向行波距離保護的優點,小波變換在行波距離保護中的套用,駐波,
簡介
電力線路在輸送電能時是以電磁波的形式傳播的,在忽略電阻和電導的情況下,其線性行波的傳播速度為:
v=1/sqrt(LC);
將線路的電感和電容代入上式,可以發現架空線路的行波傳播速度接近於光速,即v≈3*10^5km/s。
行波波長是指行波相位差正好等於2π的兩點之間的距離。
入射行波與反射行波
自傳輸線始端向終端行進的波稱為入射行波,簡稱入射波;自終端向始端行進的波稱為反射行波,簡稱反射波。在同一的正弦激勵下,這兩種波可能同時存在。它們具有同樣的
傳播速度和同樣的衰減,也具有同樣的相位變化規律,但傳播方向相反。
只呈現入射波的條件:
①傳輸線是均勻的。
②終端的負載阻抗ZL與傳槽線的特性阻抗Zc相等;或者,傳輸線電氣長度很大,以致反射波與入射波相比時可予忽略。
行波衰減和行波因子 以入射行波為例,任意點P的電壓和電流可分別表達為:
式中U1為傳輸線始端的電壓,V;a為傳輸線的衰減係數;z為P點到始端的距離;β為傳輸線的相移係數;為傳輸線的特性阻抗;為行波因子,表示該電波向+z方向行進。
性質
①電壓、電流的幅度均沿傳輸方向按指數規律下降;
②電壓、電流有相同的相位,均隨傳輸距離的延長而滯後;
③是電磁能的攜帶者,在至始端距離為z的P點,輸送的平均功率為
,
④自傳輸線任意點向終端視A的輸入阻抗均與Zc相等。
1.相速度
行波上相角
為定值的點的移動速度。相速度v
p的大小決定於波的頻率和傳輸線的相移特性:v
p=ω/β式中ω=2πf,f為信號頻率。相速度是一個有限值。對雙線傳輸線,當f>30kHz時,因
,而有
。此時,相速度將不隨信號頻率而變化。
2.相時延
由於v
p為有限值,所以信號自A點傳向B點時,需經過一段時間
才能到達。這一段時間叫作相時延。
3.波長
行波中相角差為2π的相鄰兩點間的距離稱作一個波長。波長通常用λ來表示。任一頻率的波長,都與傳輸線在該頻率下的相移係數有關:λ=2π/β
4.群速度
具有多個頻率分量的信號沿線傳輸時,如果這些頻率十分接近,它們的差值△ω大大地小於它們的中心頻率ω0,則可按下式計算其傳輸速度vg,即
並稱之為群速度。式中ω0=2πf0,f0為中心頻率;△ω=2π(△f),△f為頻頻寬度。 vg是有限值。
5.群時延
多頻信號以群速度沿線傳輸時,需經過一段時間τ
g才能到達終端,時間, τ
g稱作群時延。若距離為z,則τ
g可自下式求得:
。
行波測距式距離保護原理
高壓輸電線路是電力系統的命脈。線路發生故障後能快速地切除故障線路並及時找到故障點加以修復,是繼電保護工作者孜孜以求的目的。
然而迄今為止,輸電線路保護無論是利用工頻分量還是暫態高頻分量,都只能判斷出故障發生的區域,只能達到切除故障的目的。微機距離保護雖然能給出故障距離,但因精度不高不能滿足生產需要,要及時找到故障點對線路加以修復仍需要配備專門的故障測距裝置,兩個裝置有很多相似的功能模組,使得線路投資增加,裝置的作用得不到充分發揮。
行波距離保護由於採用輸電線路故障後的行波,使得保護裝置具有超高速動作的特性;而且利用行波折反射的特點可以精確地計算出故障距離,並同時兼作保護動作判別量和測距輸出結果,即集保護和測距為一體,有效解決了以上問題,因而行波距離保護裝置的研究極具實用價值。
利用行波進行故障測距[1]的方法早在20世紀50年代就已被提出,並在實際中得到套用。70年代末,G.W.Swift等指出了行波頻率與故障距離之間的關係[2]。1983年,P.A.Crossly等人提出了利用相關算法計算行波傳播時間進而求得故障距離,通過對故障距離和被保護線路長度的比較決定保護是否動作的行波距離保護方案[3]。1989年,我國學者根據輸電線路故障行波的特徵,提出了行波特徵鑑別式距離保護[4],該保護首先利用行波的特徵,判斷出故障發生的區間,若判斷為正方向區內故障,再進一行波特徵鑑別式距離保護。來源:
早期行波測距式距離保護的主要不足之處在於:①沒有指出正方向區外故障時保護誤動的問題;②採用相關算法提取與初始正向行波對應的反向行波誤差較大,距離計算精度不高;③由於相關算法的實質是比較兩波形的相似性,因而受線路參數的影響較大,當線路為有損或接地電阻較大時,V-、V+波形的相關性降低;④靈敏度不高,要求V-和V+信號有足夠的能量,以保證能被正確檢測。其後的研究者對行波測距式距離保護方案存在的問題提出了解決的方法[5],並對這一原理的實現做了進一步的補充[6],但因其結果不能滿足實際要求,最終沒有在實際系統中得到套用。
國內學者將現代電子技術和新興數學工具用於行波測距,使得測距精度大大提高[7,8]。行波測距裝置的成功套用無疑為進一步研製行波測距式距離保護打下了良好的基礎。
小波變換是近年來大量套用於工程計算的一種新的數學工具。實際工作表明[7,9,10]:利用小波變換提取行波信號中的故障信息不僅可以使保護的靈敏度和抗干擾能力大大提高,而且可使其不受工頻分量和線路參數等的影響。同時,隨著現代電子技術的飛速發展,高速數據採樣和處理的套用也為行波測距式距離保護的計算精度提供了保證。
行波測距式距離保護的基本原理
行波測距式距離保護是根據A型故障測距原理實現的。當輸電線路F點故障時,故障點會產生向線路兩端傳播的行波。設故障點的故障附加電壓為uf,當行波沿輸電線路傳播到達M點時(設故障發生在0時刻),在故障點處行波將再次發生折反射,這就是行波測距式距離保護的基本原理。
行波測距式距離保護的動作特性分析
行波傳播受對端母線、背側相鄰母線的影響,因而行波測距式距離保護在正方向區內、區外及反方向故障時的動作情況不盡相同。仍以圖1所示線路為例,設線上路MN的M端裝設行波距離保護,首先對區內故障的動作情況進行分析。
(1)區內故障
1)故障距離d<L/2
當故障距離小於L/2時,若不考慮相鄰母線的影響,則如式(1)~(4)所示,保護應測得實際故障距離,裝置正確動作。
2)故障距離d=L/2
設故障點產生的向對端母線運動的反向行波為un1</SUB>-=uf(t-τn)(τn為行波在故障點F和對端母線N之間的傳輸時間),對端母線的反射係數為kfn。當故障點位於線路中點時,故障點二次反射波與對端母線反射波將同時到達檢測點(τm=τn),若兩者極性相反則實際裝置中將有可能因為兩者的互相抵消而造成故障點二次反射波信號減弱,甚至可能引起保護動作失效。
3)故障距離d>L/2
故障距離大於L/2時,由於對端母線的反射波先於故障點二次反射波到達,故實際測得NF的距離。
對上述三種情況,考慮背側相鄰母線的影響,在不用方向行波的條件下,當相鄰線路長度(Lxl)小於故障距離(d)時,保護實際測得相鄰線路長度;當Lxl>d時相鄰線路對保護不造成影響。
2)區外正方向故障
對線路KM的K端保護1而言,當正方向區外F點發生故障時,其初始波頭在到達M母線處時發生折射,設其電壓折射係數為kzm,則K母線檢測到的初始和二次反向行波為
式中τmk為行波線上路MK上的傳輸時間。
由式(5)(6)可知,保護1計算出的故障距離亦滿足式(4),即所測出的故障距離為故障點到對端母線之間的距離MF。當MF的距離小於MK線路長度時,保護1會因把區外故障判斷為區內故障而誤動作。
(3)區外反方向故障
與區外正方向故障相同,在不用方向行波的條件下,當保護2的反向F點發生故障時,保護2實際測得NF距離,測距失敗;同樣,當NF距離小於NP時,保護2也會誤動作。
綜上所述,為保證在反方向故障時能正確動作,應利用方向行波實現行波測距式距離保護。
行波測距式距離保護存在的主要問題
從上述分析可以看出,對行波距離保護來說,要做到集保護和測距為一體需要解決的關鍵問題是:
1)消除對端和相鄰母線的影響,找出與初始波頭對應的故障點二次反射波頭,保證測距結果的正確性;
2)正確區分區內外故障,特別是正方向區內外故障。
另外,當故障出現在正方向出口時,受採樣率的限制,採集到的故障行波初始波頭和後續的故障點反射波頭相互疊加,由於不能正確識別故障點二次反射波,使得計算結果不正確,這說明行波距離保護線上路出口存在死區。由於這一問題不難用其它方法克服,故在此不過多討論。
方向行波距離保護的優點
1)利用正反向行波到達的先後順序判斷出故障方向,保證反方向故障時保護正確不動作。正方向故障時,反向行波或與正向行波同時到達檢測點,或先於正向行波到達(後者發生在母線上僅有兩條出線時);而反方向故障時,初始行波中只有正向行波而無反向行波,即正向行波先於反向行波到達檢測點,據此可以判斷出故障方向。
2)正向故障時,背側相鄰母線的反射波中由於只含正向行波,故不會對測距和判斷結果造成影響。
3)根據正向行波和其後續反向行波的極性關係,可以正確提取故障點二次反射波,保證其不受對端母線反射波的影響。
此外,方向行波距離保護仍存在如何區分正方向區內外故障的問題。這一問題可考慮用零模分量解決。眾所周知,零模分量的傳播速度與線模是不同的,因而初始波頭中線模和零模到達檢測點的時間也就不同,它們的時間與速度存在關係:t0=d/v0,tα=d/vα,其中d為故障距離。用t0、v0、tα、vα表示d得到:
只用初始波頭中線模和零模的行波信息就可以求出故障距離。這種方法雖然可行,但仍有其局限性:
1)零模分量在實際傳輸中衰減很快且速度隨頻率的變化會發生變化,因而只適用於較短的線路。
2)由於兩相短路故障時沒有零模分量出現,因而這一方法只適用於接地故障。
綜上所述,對於方向行波測距式距離保護來說,如何正確區分正向區內和區外故障仍是一個有待解決的重要問題。不藉助通信手段,利用單端量所測得的行波信息來區分區內、外故障是一個很值得深入研究的課題。
小波變換在行波距離保護中的套用
與相關算法相比較小波變換具有良好的消噪功能和分頻特性;特別地,由於它具有良好的時頻局部化性能,因而能準確捕捉到各次行波到達的時刻,比起相關算法來說其可靠性更高。
1.利用分頻特性提取行波信息
由多分辨分析理論可知,隨著尺度參數a的二進膨脹,信號被逐漸地分解到每一個小波空間;同時小波的時頻局部化性質說明,當a增大時,對應的中心頻率會逐漸降低,這說明尺度較小時對應的小波空間的頻帶較高,隨尺度的增大,對應小波空間的頻帶逐步降低。當採用二進小波變換時,尺度參數以2的倍數增大,所以頻帶以2的倍數降低。因此小波變換可以把一個信號分解成為若干個互不重疊的頻帶的信號。這樣在對某一尺度的小波變換結果進行分析時,就相當於對其它頻率進行了完全濾波,這樣既可以避免為提取行波信號而造成的裝置和算法的複雜性,又可以保證行波保護不受工頻分量的影響。
2.利用奇異性檢測定位行波波頭
行波距離保護利用波頭到達時刻計算故障距離,而小波變換的模極大值與信號的奇異點對應,因而利用小波變換可以對行波波頭進行準確定位,從而保證測距結果的精度。
駐波
波在一個空間中來回反射,由於來回的距離等於1/4波長的奇數倍,於是反射回來的波與後面傳來的波發生干涉,形成穩定的干涉場,各處的振幅穩定不變。振幅為零的地方叫波節,振幅最大的地方叫波腹。有這種經驗:(如果實在沒有,回家試試,2-3米長的繩子。)在一根繩子上固定一端不動,我們不停地抖繩子另一端,並且改變快慢,在一種速度下,就會在繩子看到一個穩定的象蓮藕一樣的圖像,似乎波"停止“了傳播,所以叫駐波(駐留的波)。