基本介紹
- 中文名:萊文斯坦距離
- 外文名:Levenshtein distance
介紹,定義,性質,套用,算法,
介紹
萊文斯坦距離(LD)用於衡量兩個字元串之間的相似度。 以下我們稱這兩個字元串分別為 和
和 。萊文斯坦距離被定義為''將字元串
。萊文斯坦距離被定義為''將字元串 變換為字元串
變換為字元串 所需的刪除、插入、替換操作的次數''。
所需的刪除、插入、替換操作的次數''。




萊文斯坦距離以俄國科學家Vladimir levenshtein命名,他於1965年發明了這個算法。 如果你對Levenshtein這個詞的發音有問題,也可以稱這個距離為編輯距離。
定義
在數學上,兩個字元串a,b的萊文斯坦距離記作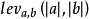 。這裡
。這裡
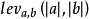

這裡, 和
和 分別表示字元串a和b的長度,
分別表示字元串a和b的長度,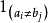 是當
是當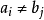 時值為1,否則值為0的示性函式。這樣,
時值為1,否則值為0的示性函式。這樣,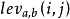 是
是 的前
的前 個字元和
個字元和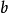 的前
的前 個字元之間的距離。
個字元之間的距離。


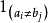
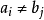
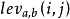


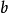

性質
萊文斯坦距離有一些簡單的上下界,如
:
- 萊文斯坦距離至少是兩個字元串長度的差值
- 萊文斯坦距離不大於較大的那個字元串的長度
- 如果兩個字元串相等,那么它們的萊文斯坦距離為0
- 如果兩個字元串等長,那么它們的漢明距離是萊文斯坦距離的上界
- 兩字元串的萊文斯坦距離不大於它們與第三個字元串的萊文斯坦距離之和(三角性)
套用
算法
動態規劃經常被用來作為這個問題的解決手段之一。
int LevenshteinDistance(string str1[1..lenStr1], string str2[1..lenStr2]) int d[0..lenStr1, 0..lenStr2] int i, j, cost for i = 0 to lenStr2 d[i, 0] := i for j = 0 to lenStr1 d[0, j] := j for i = 1 to lenStr2 for j = 1 to lenStr1 if str2[i-1] = str1[j-1] cost := 0 else cost := 1 d[i, j] := min( d[i-1, j ] + 1, // 刪除 d[i , j-1] + 1, // 插入 d[i-1, j-1] + cost // 替換 ) return d[lenStr1-1, lenStr2-1]

