荷蘭學者范第姆特(van Deemter)等吸收塔板理論中的一些概念,並進一步把色譜分配過程與分子擴散和氣液兩相中的傳質過程聯繫起來,建立了色譜過程的動力學理論,即速率理論。速率理論認為,單個組分分子在色譜柱內固定相和流動相間要發生千萬次轉移,加上分子擴散和運動途徑等因素,它在柱內的運動是高度不規則的,是隨機的,在柱中隨流動相前進的速率是不均一的。與偶然誤差造成的無限多次測定的結果呈常態分配相類似,無限多個隨機運動的組分粒子流經色譜柱所用的時間也是常態分配的。tR是其平均值,即組分分子的平均行為。
速率理論更重要的貢獻是提出了范第姆特方程式。它是在塔板理論的基礎上,引入影響板高的動力學因素而導出的。它表明了塔板高度(H)與載氣線速(u)以及影響H的三項因素之間的關係,其簡化式為
H=A+B/u+Cu (12-18)
式中A、B、C為常數:A項稱為渦流擴散項,B/u項稱為分子擴散項,Cu項稱為傳質項;u為載氣線速率,即一定時間裡載氣在色譜柱中的流動距離,單位為cm/s。由式中關係可見,當u一定時,只有當A、B、C較小時,H才能有較小值,才能獲得較高的柱效能;反之,色譜峰擴張,柱效能較低,所以A、B、C為影響峰擴張的三項因素。
基本介紹
- 中文名:速率理論
- 外文名:rate theory
- 提出者:范第姆特
- 國籍:荷蘭
- 表達式:H=A+B/u+Cu
渦流擴散項A,分子擴散項B/u,傳質阻力項Cu,范第姆特方程,
渦流擴散項A
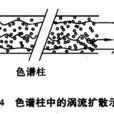
在填充色譜柱中,氣流碰到填充物顆粒時,不斷改變方向,使試樣組分在氣相中形成紊亂的類似渦流的流動。從而導致同一組分分子所通行路途的長短不同,因此它們在柱中停留的時間也不相同,它們是分別在一個時間間隔內到達柱尾,故因擴散而引起色譜峰的擴張。這種擴散稱為渦流擴散(eddy diffusion),如圖12-4所示。A稱為渦流擴散項,它與填充物的平均顆粒直徑大小和填充物的均勻性有關。
A=2λdp (12-19)
式中,λ為填充不規則因子,dp為顆粒的平均直徑。由上式可見,A與載氣性質、線速度和組分無關。裝柱時應儘量填充均勻,並且使用適當大小的的粒度和顆粒均勻的載體,這是提高柱效能的有效途徑。對於空心毛細管柱,由於無填充物,故A等於零。
分子擴散項B/u
分子擴散又稱為縱向擴散(longitudinal diffusion),由於組分在色譜柱中的分布存在濃度梯度,濃的部分有向兩側較稀的區域擴散的傾向,因此運動著的分子形成縱向擴散。分子擴散項與載氣的線速(u)呈反比,載氣流速越小,組分在氣相中停留時間越長,分子擴散越嚴重,由於分子擴散引起的峰擴張也越大。為了減小峰擴張,可以採用較高的載氣流速,通常為0.01~1.0cm/s。
B稱為分子擴散係數,與組分在載氣中的擴散係數有關
B=2γDg (12-20)
式中γ稱為彎曲因子,是因柱內填充物而引起的氣體擴散路徑彎曲的因數,Dg為組分在氣相中的擴散係數。Dg與載氣相對分子質量的平方根呈反比,所以對於既定的組分採用相對分子質量較大的載氣,可以減小分子擴散,對於選定的載氣,則相對分子質量較大的組分會有較小的分子擴散。Dg隨柱溫的升高而加大,隨柱壓的增大而減小。彎曲因子是與填充物有關的因素,在填充柱內,由於填充物的阻礙,不能自由擴散,使擴散路徑彎曲,擴散程度降低,故γ<1.對於空心毛細管柱,由於沒有填充物的存在,擴散程度最大,故γ=1.可見,在色譜操作時,應選用相對分子質量大的載氣、較高的載氣流速、較低的柱溫,這樣才能減小B/u的值,提高柱效率。
傳質阻力項Cu
在氣液填充柱中,試樣被載氣帶入色譜柱後,組分在氣液兩相中分配而達平衡,由於載氣流動,破壞了平衡,當純淨載氣或含有組分的載氣(濃度低於平均濃度)來到後,則固定液中組分的部分分子又回到氣液界面,並逸出而被載氣帶走,這種溶解、擴散、平衡及轉移的過程稱為傳質過程。影響此過程進行速率的阻力,稱為傳質阻力(mass transfer resistance)。傳質阻力包括氣相傳質阻力和液相傳質阻力。傳質阻力項(Cu)中的C為傳質阻力係數,該係數實際上為氣相傳質阻力係數(Cg)和液相傳質阻力係數(CL)之和,即
C=Cg+CL
(1)氣相傳質過程。指試樣組分從氣相移動到固定相表面的過程。在這一過程中,試樣組分將在氣液兩相間進行質量交換,即進行濃度分配。若在這個過程中進行的速率較緩慢,就會引起譜峰的擴張。氣相傳質阻力係數為
Cg=0.01k2dp2/((1+k)2Dg) (12-21)
式中k為容量因子。由上式可見,氣相傳質阻力係數與固定相的平衡顆粒直徑平方成正比,與組分在在其中的擴散係數成反比。在實際色譜操作過程中,應採用細顆粒固定相和相對分子質量小的氣體(如H2、He)作載氣,可降低氣相傳質阻力,提高柱效率。
(2)液相傳質過程。指試樣組分從固定相的氣液界面移到液相內部,並發生質量交換,達到分配平衡,然後又返回到氣液界面的傳質過程。若這過程需要的時間長,表明液相傳質阻力就越大,就會引起色譜峰的擴張。液相傳質阻力係數為
CL=2kdf2/(3(1+k)2DL)(12-22)
式中df為固定相的液膜厚度,DL為組分在液相中的擴散係數。從式(12-22)可見,CL與固定相的液膜厚度(df)的平方成正比,與組分在液相中的擴散係數(DL)成反比。在實際工作中減小CL的主要方法為:(i)降低液膜厚度,在能完全均勻覆蓋載體表面的前提下,適當減少固定液的用量,使液膜薄而均勻;(ii)通過提高柱溫的方法,增大組分在液相中的擴散係數(DL)。這樣就可降低液相傳質阻力,提高柱效。
當固定液含量較大,液膜較厚,中等線性流速(u)時,塔板高(H)主要受液相傳質阻力的影響,而氣相傳質阻力的影響較小,可忽略不計。但用低含量固定液的色譜柱,高載氣流速進行快速分析時,氣相傳質阻力就會成為影響塔板高度的重要因素。
將A、B、C的關係式代入簡式(式12-18),得
H=2λdp+2γDg/u+(0.01k2dp2/(1+k)2Dg+2kdf2/3(1+k)2DL)u (12-23)
由以上討論可以看出,范第姆特方程是色譜工作者選擇色譜分離條件的主要理論依據,它說明了色譜柱填充的均勻程度、載體粒度的大小、載氣種類和流速、柱溫、固定相的液膜厚度等因素對柱效能及色譜峰擴張的影響,從而對於氣相色譜分離條件的選擇具有指導意義。
以上速率理論主要是針對氣相色譜法來討論的,速率理論對於液相色譜法、高效液相色譜法也均適用,但因流動相是液體而不是氣體,也有一些與氣相色譜法不同之處。
范第姆特方程
圖12-5是氣相色譜法和高效液相色譜法的H-u曲線。由圖可見,兩者形狀明顯不同。高效液相色譜法接近一條直線,而氣相色譜法曲線中有一極小值。在HPLC中,由於流動相是液相,影響柱效的因素與GC不完全相同,因此,范第姆特方程有一些區別。(註:不知什麼原因,圖片無法顯示,望知友補充)。
在范第姆特方程中,HPLC與GC的渦流擴散項完全相同(即式12-19)。
HPLC的分子擴散項是因同種組分分子由濃度大的譜帶中心向濃度較低的兩邊擴散所引起。它與組分分子在流動相中的擴散係數(Dm)成正比,與流動相的平均線速(u)成反比。
B/u=CdDm/u (12-24)
式中Cd為常數。
由於液相中擴散係數要比氣相中小4~5個數量級,HPLC中該項對於譜帶擴張的影響可以忽略不計。這就是圖12-5中HPLC的曲線沒有極小值的原因。
HPLC的傳質阻力是由於組分在兩相間的傳質過程實際上不能瞬間達到平衡而引起的,其傳質阻力包括三項:固定相傳質阻力(Hs),移動流動相傳質阻力(Hm)和滯留流動相傳質阻力(Hsm),即
Cu=Hs+Hm+Hsm (12-25)
(1)固定相傳質阻力項。主要發生在分配色譜法中,與氣相色譜法中液相傳質阻力項相同,即
Hs=Csdf2u/Ds (12-26)
式中df為固定液塗層厚度,Ds為組分在固定液中的擴散係數,Cs為常數。由式(12-26)可見,較薄的固定液塗層時,Hs較小。
(2)移動流動相的傳質阻力項。它是由於同一流路中靠近固定相表面處流速較慢而流路中心流速較快而造成的(見圖12-6a),其表達式為
Hm=Cmdp2u/Dm(12-27)
式中dp為填充物平均顆粒直徑,Dm為組分在流動相中的擴散係數,Cm為常數。顯然填料顆粒越小,即流路越窄,Hm就越小。
(3)滯留流動相的傳質阻力項。固定相的多孔性,使一部分流動相滯留在固定相微孔內。流動相中的試樣分子要與固定相進行傳質,必須先擴散到滯留區。孔有深度,且擴散路徑不同就造成了譜帶擴張,其表達式為
Hsm=Csmdp2u/Dm (12-28)
式中Csm是與顆粒微孔和容量因子有關的常數。
氣相色譜法主要考慮固定相的傳質阻力;液相色譜法與之不同,在整個傳質過程中起主要作用的是流動相傳質阻力,特別是滯留流動相的傳質阻力,因此,改進固定相結構,減小滯留流動相傳質阻力是提高液相色譜柱效的關鍵。
以上各項可以歸納為:
H=2λdp+CdDm/u+(Csdf2/Ds+Cmdp2/Dm+Csmdp2/Dm)u (12-29)
其中CdDm/u項實際上可以略去。於是,上式可簡寫為:
H=A+Cu (12-30)
總上所述,要想提高液相色譜法的柱效,必須用小而均勻的固定相顆粒填充均勻,以減小渦流擴散和流動相傳質阻力。改進固定相的結構,對於減小滯留流動相傳質阻力以及固定相傳質阻力至關重要。此外,選用低粘度的流動相(如甲醇、乙腈等),也有利於減小傳質阻力,提高柱效。