范德瓦耳斯狀態方程

范德瓦爾斯狀態方程是荷蘭物理學家范德瓦爾斯於1873年提出的一種實際氣體狀態方程。是對理想氣體狀態方程的一種改進，特點在於將被理想氣體模型所忽略的的氣體分子自身大小和分子之間的相互作用力考慮進來，以便更好地描述氣體的巨觀物理性質。

基本介紹

• 中文名：范德瓦爾斯狀態方程
• 外文名：van der Waals equation of state 
• 提出者：范德瓦爾斯
• 提出時間：1873年

釋義

1873年范德瓦爾斯針對理想氣體模型的兩個假定(分子自身不占有體積；分子之間不存在相互作用力)，考慮了分子自身占有的體積和分子間的相互作用力，對理想氣體狀態方程進行了修正。分子自身占有的體積使其自由活動空間減小，在相同溫度下分子撞擊容器壁的頻率增加，因而壓力相應增大。如果用V_m-b表示每摩爾氣體分子自由活動的空間，參照理想氣體狀態方程，氣體壓力應為p=RT/(V_m-b)。另一方面，分子間的相互吸引力使分子撞擊容器壁面的力量減弱，從而使氣體壓力減小。壓力減小量與一定體積內撞擊器壁的分子數成正比，又與吸引它們的分子數成正比，這兩個分子數都與氣體的密度成正比。因此，壓力減小量應與密度的平方成正比，也就是與摩爾體積的平方成反比。

方程形式

范德華方程具體形式為：

式中，a、b分別為對氣體壓力和體積校正的相關常量，稱為范德華常量。每種氣體的a、b都有各自的特定值。

適用範圍

范氏方程對氣-液臨界溫度以上流體性質的描寫優於理想氣體方程。對溫度稍低於臨界溫度的液體和低壓氣體也有較合理的描述。但是，當描述對象處於狀態參量空間(P，V，T)中氣液相變區（即正在發生氣液轉變）時，對於固定的溫度，氣相的壓強恆為所在溫度下的飽和蒸氣壓，即不再隨體積V（嚴格地說應該是單位質量氣體占用的體積，即比容）變化而變化，所以這種情況下范氏方程不再適用。

范德瓦爾斯常量

下表列出了部分氣體的a，b 的值：

氣體	a / (atm·L/mol)	b / (L/mol)
氫	0.191	0.0218
氧	1.360	0.03183
氮	1.390	0.03913
氯	6.493	0.05622
氦	0.03412	0.02370
氖	0.2107	0.01709
汞蒸氣	8.093	0.01696
二氧化碳	3.592	0.04267
水蒸氣	5.464	0.03049

范德瓦爾斯定溫線

范德瓦爾斯方程的引出，是從理論分析出發導出氣體狀態方程的一個典型例子。范德瓦爾斯方程只不過是用兩個常數很粗略地考慮了氣體內分子運動的行為，所以還不能精確地表述氣體的p-V-T關係。但是，它為用理論方法研究狀態方程開拓了道路。特別是它在定性上能反映出物質氣—液相變的性質。按照范德瓦爾斯狀態方程在p-V圖上作出的定溫線稱為范德瓦爾斯定溫線。

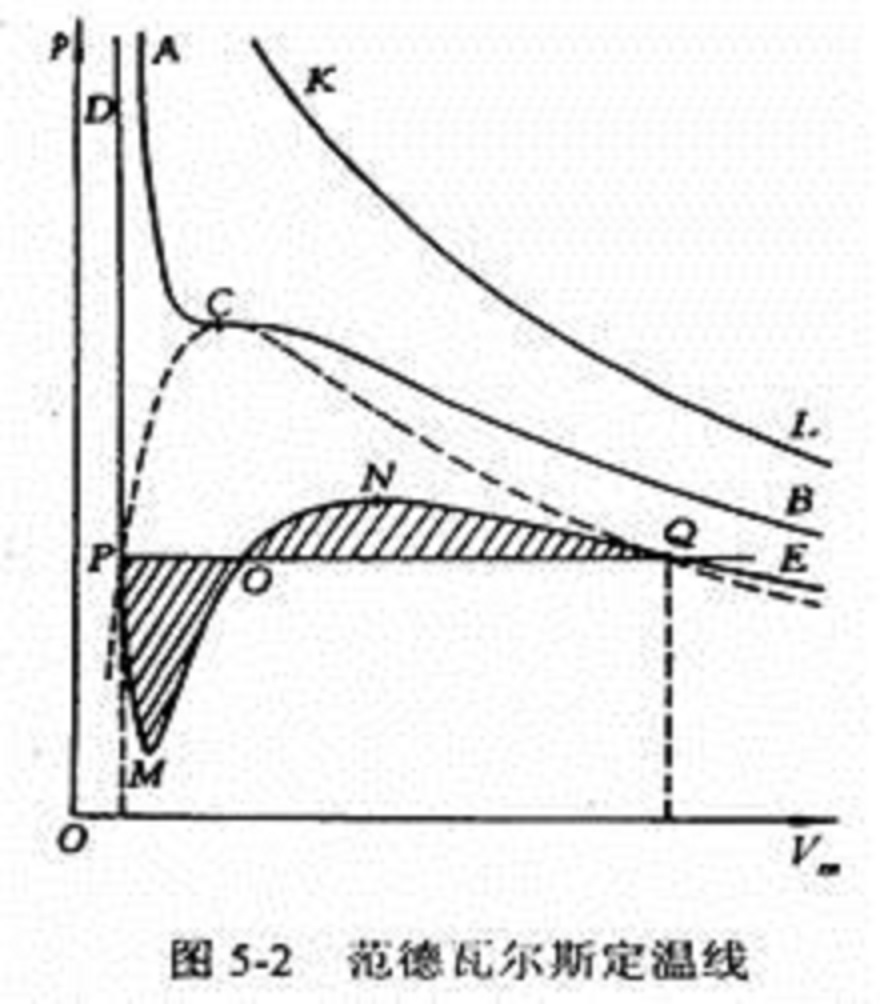
范德瓦爾斯定溫線

范德瓦爾斯定溫線在不同的溫度範圍內有圖5-2所示的三種類型。

第一種是在溫度較低的範圍內，定溫線如曲線DPMONQE所示。它有一個極小值點M和一個極大值點N。直線POQ與曲線的轉折部分圍成兩塊相等的面積PMOP與ONQO。這樣，DP段對應於液體狀態；QE段對應於氣體狀態；而P、Q兩點分別對應於飽和液及飽和氣狀態。一般實驗測定的液—氣相變是沿直線P-Q進行的。雖然范德瓦爾斯方程給出的相轉變過程PMONQ與實驗測定的存在偏差，但在精確的實驗中仍可觀測到PM中鄰近P點的一段，和QN中鄰近Q點的一段，即所謂過熱液及過冷氣階段。

第二種類型如圖5-2中曲線ACB所示。它是由第一種曲線隨著溫度的升高，其中極小值點M與極大值點N逐漸接近，當溫度升至某一定值時兩極值點重合而形成的曲線。這條曲線對應的溫度稱為臨界溫度，極值點重合點C稱為臨界點，它是臨界定溫線上的拐點。

第三種類型的曲線如圖5-2中曲線KL所示，它對應的溫度高於臨界溫度。曲線上不存在極值點及拐點，這表明，在溫度高於臨界溫度的範圍內物質總是呈現為氣態。