基本介紹
- 中文名:
- 外文名:
- 套用學科:
- 特點:
定義
線性系統
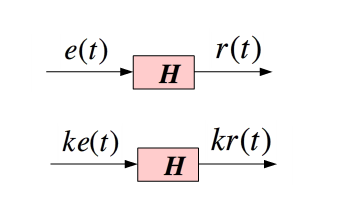
不變系統


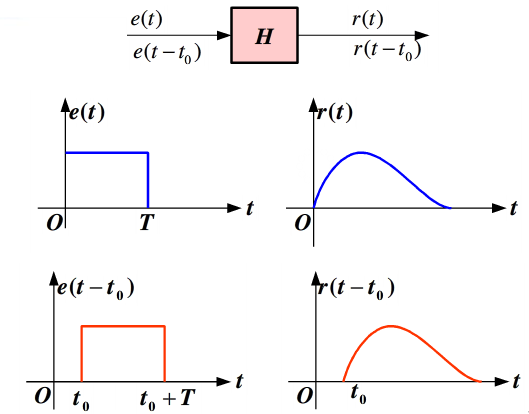




線性非移變系統(linear shift-invariant system) 線性系統的輸出回響與輸入信號之間呈線性關係。亦稱線性移不變系統。因此,滿足疊加性與齊次性。定義若y1(n)及y2(n)分別為某系統對輸入信號x...
線性非移變系統並聯(parallel combination oflinear shift-invariant system)系統之間的一種連結方式.兩個線性非移變離散系統h,(n)和hz(n),如果按照圖1所示方式連結,則稱為線性非移變離散系統的並聯.並聯之後仍構成一個線性非移變離散...
線性非移變系統級聯是系統之間的一種連結方式。線性非移變系統級聯(cascade combination oflinear shift-invariant system)系統之間的一種連結方式.兩個線性非移變系統h,(n)和(hzCn),如果按照方式連結,則稱為線性非移變系統級聯....
模擬系統(analog system)是用以研究信息理論和方法的系統之一,指輸入信號與輸出信號都是模擬信號的系統,它由模擬器件構成。對於具有穩定性和因果性的線性非移變模擬系統,可用其單位衝激回響h(t)來完全表征,也可用其傳輸函式H (s)來...
非移變系統(shift-invariant system)一種信號變換系統.非移變系統(shift-invariant system)一種信號變換系統.系統的輸人與輸出特性不隨時間(獨立變數)的起點變化而變化,即:如果y(n)是系統對於二((n)的回響,則y(n-k)就是該...
線性系統對隨機信號回響(response of lin-ear system to random signal)線性系統分析中的基本概念。對於穩定的線性非移變系統,如果輸人隨機過程是平穩的,則輸出隨機過程也是平穩的.如果輸人隨機過程的均值為m”則輸出隨機過程的均值為m...
因果性(causality),是一種只有在輸入信號激勵下才能產生輸出回響的性質。一個系統如果符合因果性,那么該系統輸出信號不會超前於輸入信號而產生。即如輸入信號在n 對於線性非移變系統,它的因果性可以定義為該系統滿足n 幾乎所有實際運行...
2.3.1 線性非移變系統 2.3.2 系統的穩定性和因果性 2.3.3 線性常係數差分方程 2.4 離散時間信號和系統的頻域描述 2.4.1 離散時間信號的傅立葉變換(DTFT)2.4.2 離散時間信號的傅立葉變換的性質 2.4.3 離散時間系統的...
2.3.4 線性非移變系統的性質19 2.3.5 穩定系統20 2.3.6 因果系統20 2.4 線性常係數差分方程21 2.4.1 線性常係數差分方程21 2.4.2 線性常係數差分方程的求解22 2.4.3 用差分方程表示濾波器系統22 2.5 ...
我們可將語音信號看成準周期序列或隨機噪聲序列作為激勵的線性非移變系統的輸出,此模型可分為三個部分:激勵模型、聲道模型、輻射模型。語音信號模型 激勵模型 a.濁音激勵:氣流在通過繃緊聲帶時,衝激聲帶產生振動,使聲門處形成周期性的...
2.3.4 線性非移變系統的性質 2.3.5 穩定系統 2.3.6 因果系統 2.4 線性常係數差分方程 2.4.1 線性常係數差分方程 2.4.2 線性常係數差分方程的求解 2.4.3 用差分方程表示濾波器系統 2.5 離散時間信號與系統時域分析...
2.1.1 連續時間系統的線性非移變特性 2.1.2 連續信號的時域分解 2.1.3 卷積法求系統零狀態回響與卷積的性質 2.2 周期信號的頻譜分析——傅立葉級數 2.2.1 正交函式 2.2.2 三角函式形式的傅立葉級數 2.2.3 指數形式的...
線性非移變系統 以果性 穩定性 取樣定理 混疊 2變換 離散傅立葉變換 線性卷積 周期卷積 循環卷積 重疊保留法 重疊相加法 快速傅立葉變換 時間抽選算法 頻率抽選算法 線性調頻z變換 同址計算 倒位序 基-r算法 蝶形計算 取洋數據...
4.1 線性非移變離散系統 4.2 離散系統的時域分析 4-3 離散系統的z域分析 習題 第5章 離散時間信號分析 5.1 序列的傅立葉變換 5.2 信號的傅氏、拉氏及z變換間的關係 5.3 離散傅立葉級數(DFS)5.4 離散傅立葉變換(DFT)5...
1.5常係數線性差分方程 1.5.1線性非移變離散系統的數學模型 1.5.2遞推法 1.5.3經典法 1.6數位化處理方法 1.6.1時域採樣 1.6.2原信號的恢復(插值)1.6.3數位化處理方法 習題 第2章z變換與離散系統的頻域分析 2.1z...
