使用二次型性能指標的線性系統最優控制。
基本介紹
- 中文名:線性二次型最優控制
- 外文名:linear quadratic optimal control
- 學科:電力科學
- 拼音:xianxing ercixing...
定義,性能指標,狀態調節器問題,最優控制規律,跟蹤問題,
定義
使用二次型性能指標的線性系統最優控制。它可得到狀態線性反饋的最優控制規律,便於實現閉環最優控制,是套用廣泛的最優控制方式。
性能指標
線性系統狀態方程及輸出方程為
x(t)=A(t)x(t)+B(t)u(t) (1)
y(t)=C(t)x(t) (2)
式中x(t)為n維狀態向量;u(t)為p維控制向量;y(t)為q維輸出向量。設z(t)為理想輸出向量,與y(t)同維數,並定義
e(t)=z(t)-y(t) (3)
誤差向量。線性二次型最優控制問題的性能指標為
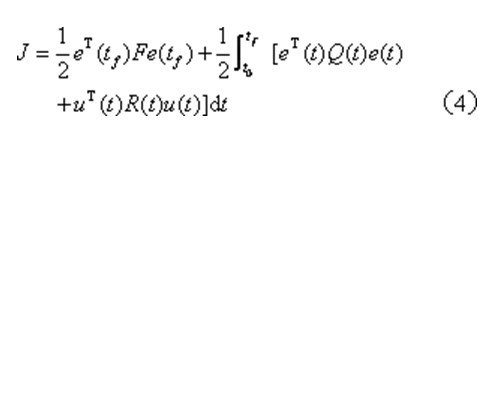
這裡,權函式F、Q(t)為正半定矩陣,R(t)為正定矩陣。假設tf固定。要求尋找最優控制u*(t),使性能指標J為最小。被積函式的第一項表明誤差e(t)的大小,是非負的。其第二項表明控制功率的大小,對應於u≠0它恆為正。因此,對u(t)往往不需再加約束,而常設u(t)為自由的。性能指標的第一項則表示終值誤差。
狀態調節器問題
系統狀態方程如式 (1)所示,u(t)不受約束,tf固定,性能指標為
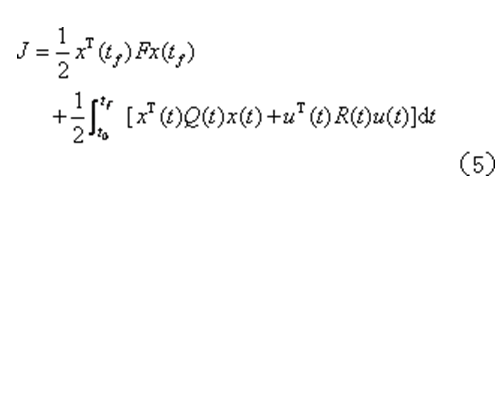
尋找最優控制u*(t),使性能指標J為最小。
用極小值原理或動態規劃法,可得下列矩陣黎卡提微分方程(一階非線性微分方程)
P(t)=-P(t)A(t)-AT(t)P(t)+P(t)B(t)R-1(t)BT(t)P(t)-Q(t) (6)
其邊界條件為
P(tf)=F (7)
由式(6)解出P(t)後,可得最優控制規律為
u*(t)=-R-1(t)BT(t)P(t)x*(t) (8)
由式(8)可以看出,最優控制規律是一個狀態線性反饋規律,控制向量u*(t)由狀態向量x*(t)生成,構成狀態反饋,並且呈線性關係。這樣,能方便地實現閉環最優控制,這一點在工程上具有十分重要的意義。
P(t)是一對稱矩陣,一般都要由計算機求出方程(6)的數值解。P(t)是時間函式,即使線性系統是定常的,為了實現最優控制,反饋增益應該是時變的,而不是常值反饋增益。這一點與經典控制方法的結論有本質的差別。
可以求得性能指標的最小值為
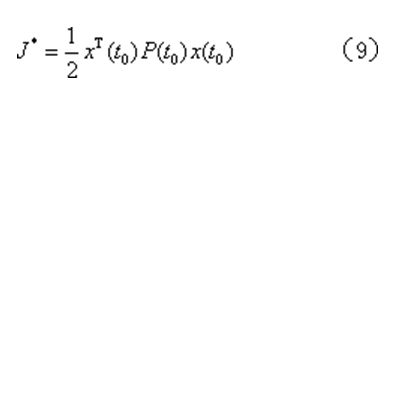
tf=∞時的狀態調節器問題 定常系統方程為
x(t)=Ax(t)+Bu(t) (10)
這裡,A、B為常值矩陣,u(t)不受約束,性能指標為

Q、R為常值矩陣,Q為正半定的,R為正定的。求最優控制u*(t),使性能指標J為最小。
對於這樣的系統,有(t)=0情況下的矩陣黎卡提方程

上式是矩陣黎卡提代數方程,它是非線性方程。求解該方程,可得最優控制為
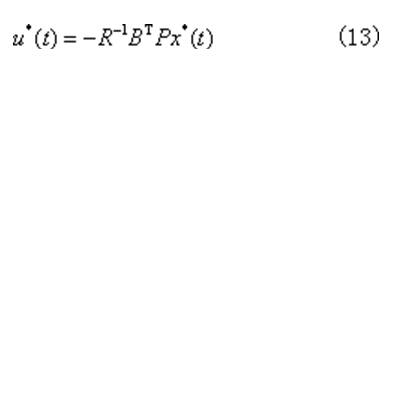
性能指標的最小值也由式(9)求得。
輸出調節器問題 系統動態方程為式(1)、(2),u(t)不受約束,tf固定,性能指標為
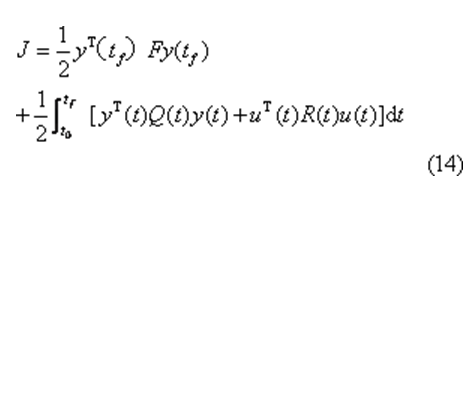
式中F和Q(t)為正半定矩陣;R(t)為正定矩陣。求最優控制u*(t),使性能指標J為最小。
可將這類問題轉化成等效的狀態調節器問題,得:若且唯若系統完全可觀測時,存在唯一的最優控制
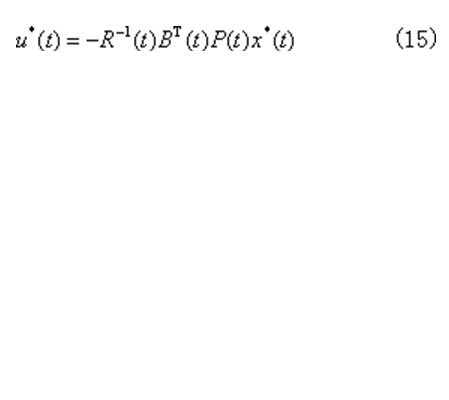
其中,P(t)滿足下列矩陣黎卡提方程
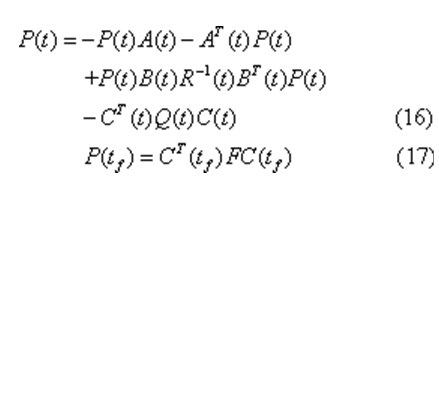
最優控制規律
輸出調節器的最優控制規律,並不是輸出量y(t)的線性反饋,而仍是狀態x(t)的線性反饋。僅由輸出反饋時,沒有充分利用全部信息,不能構成最優控制。
完全可控、可觀測的定常系統,tf=∞時的輸出調節器問題,其最優控制存在並且是唯一的
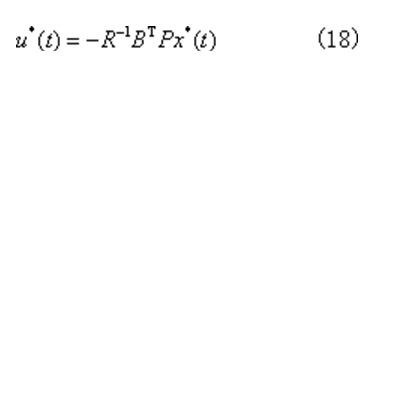
P為下列矩陣黎卡提代數方程的解

跟蹤問題
系統動態方程為式(1)、(2),x(t0)=x0,系統完全可觀測,理想輸出為z(t),誤差向量為式(3),性能指標為式(4),u(t)不受約束,tf固定,求最優控制u*(t),使性能指標J為最小。
用極小值原理來求解,並設
λ*(t)=P(t)x*(t)-g(t) (20)
可寫出形如式(16)的黎卡提方程以及下式
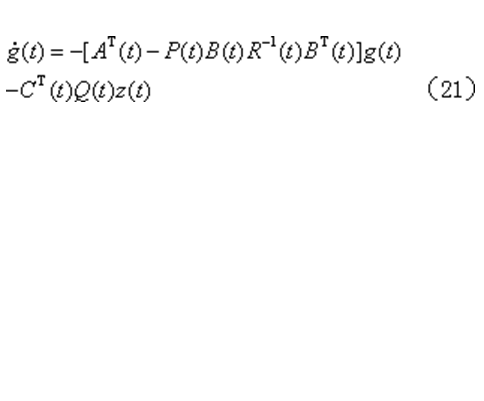
其邊界條件為
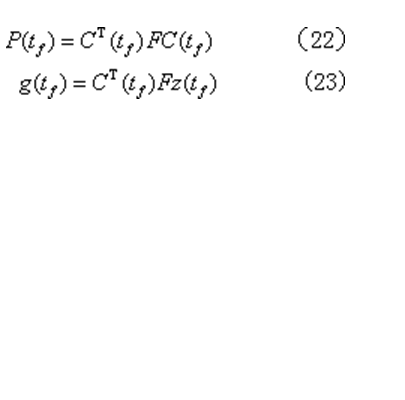
從而得最優控制規律
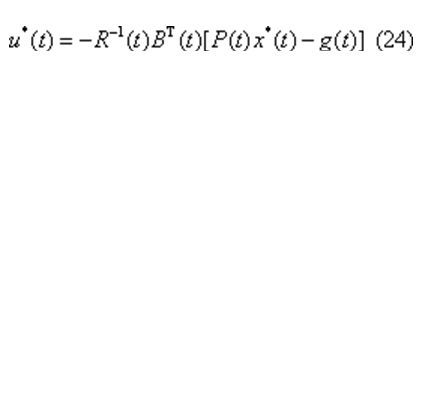
對於線性定常系統,當理想輸出z(t)為常值、終端時刻tf極大但不為無窮大時,可以導出一個近似的最優控制規律如下,它具有很大的實用意義。
設系統狀態方程如式(10)所示,x(t0)=x0,輸出方程y(t)=Cx(t),系統完全可控並完全可觀測,理想輸出z(t)=z0,tf足夠大,性能指標為
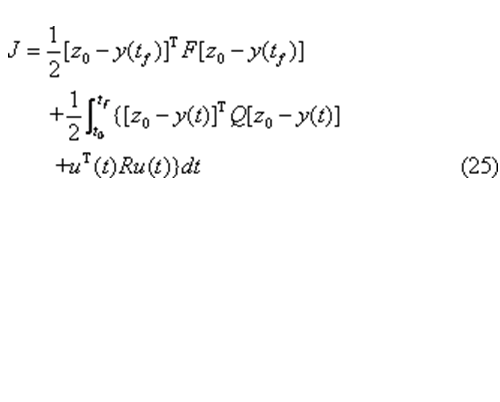
則其最優控制存在並唯一,為

其中P和g依次滿足下列兩式


