網球拍定理

以網球拍為例可以出色地說明剛體具有不相等主慣性矩時其歐拉方程的解，稱之為網球拍定理。

基本介紹

• 中文名：網球拍定理
• 外文名：Tennis racket theorem
• 所屬領域：物理
• 目的：討論歐拉不對稱陀螺運動穩定
• 別名：賈尼別科夫定理
• 提出時間：1985年

判定內容

網球拍的三個主軸易於判定如下：(1)沿把柄(2)垂直於把柄並在網的平面內(3)垂直於把柄和網，當使網球拍繞其主軸之一旋轉的同時並把球拍拋入空中時，就會看到一種奇特的現象。如果初始旋轉是繞著軸(1)或軸(3)，則拍子將繼續繞初始軸均勻旋轉，並且能很容易地再抓住。另一方面，如果起始是繞軸(2)旋轉，則運動很快地變成不規則的，旋轉演變成繞全部三個主軸進行，使得難以抓住下落的球拍，根據歐拉方程就可以解釋所觀察到的行狀。為了把歐拉方程套用於網球拍，我們選擇球拍的質心做為主軸坐標系的原點。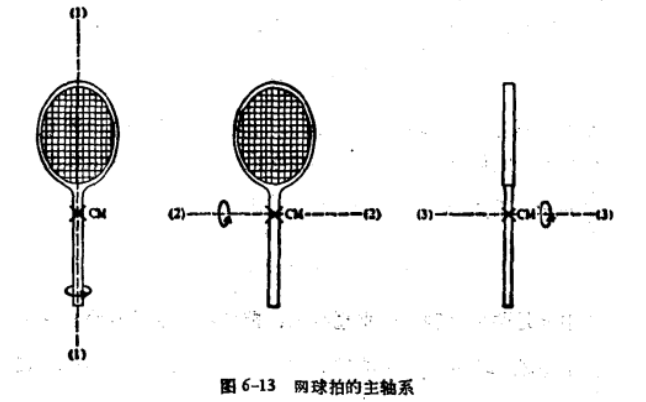

原理

下面我們利用歐拉動力學方程來討論歐拉不對稱陀螺運動的穩定性問題。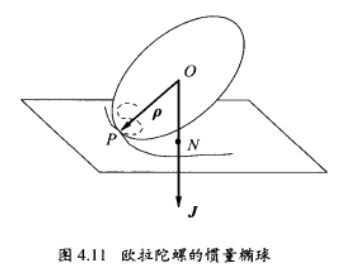

設陀螺的3個主轉動慣量互不相等，不妨設，I₁>I₂>I₃，慣量橢球為三軸橢球，如果陀螺繞3個主軸之一轉動，則切點P與N點重合，空間極跡與本體極跡均退縮為一點，剛體的轉軸保持不變，這是一種動平衡，轉動的穩定性是指：如果轉軸稍微偏離慣量主軸，這種偏離是否能夠限制在一定的範圍內，而不至越來越大?

(i)我們先看對於X₃軸的微小偏離，這時在歐拉動力學方程中 ， 為小量：

從而 為常數。由歐拉方程可知，I₃小於I₁和I₂，所以 ， 不會越來越大，運動是穩定的。

(ii)再看轉軸稍微偏離X₁軸的情形，此時，為小量，近似為常數，採用類似於(i)的步驟，可得：

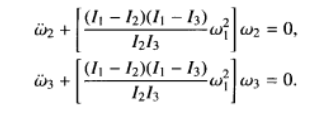
此時方括弧內的常數大於零，故 ，有振盪解，運動仍然是穩定的。

(iii)最後看轉軸x₂軸有微小偏離的情形，在這種情形中 ，為小量，故 為常數，此時有：

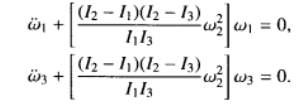
因I₂小於I₁，大於I₃，方括弧內常數小於零，方程的解 ，呈指數形式，故轉動是不穩定的。

綜上可得出結論：自由剛體繞主轉動慣量最大或最小主軸的轉動是穩定的，繞另一個主軸的轉動不穩定，這一結論稱為網球拍定理，這種效應很容易通過網球拍繞自身3個主軸的轉動演示出來，這是因為在地球表面附近，重力是均勻分布的，所以球拍對於質心沒有重力矩，如果略去風的阻力矩不計，則網球拍可視為一個歐拉不對稱陀螺。