結構可靠度是在規定的時間和條件下,工程結構完成預定功能的機率,它是工程結構可靠性的機率度量。為了保證結構的安全、適用和經濟,在設計時需要進行結構可靠度分析。
基本介紹
- 中文名:結構可靠度分析
- 外文名:structural reliability
極限狀態
 極限狀態方程
極限狀態方程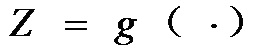 結構的功能函式
結構的功能函式 極限狀態方程2
極限狀態方程2可靠度與失效機率
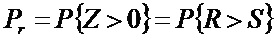 可靠度
可靠度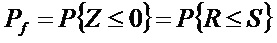 失效機率
失效機率 失效機率和可靠度的互補關係
失效機率和可靠度的互補關係 機率密度函式
機率密度函式 均值
均值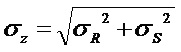 標準差
標準差 結構可靠度
結構可靠度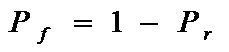 結構失效機率
結構失效機率結構可靠度是在規定的時間和條件下,工程結構完成預定功能的機率,它是工程結構可靠性的機率度量。為了保證結構的安全、適用和經濟,在設計時需要進行結構可靠度分析。
 極限狀態方程
極限狀態方程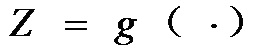 結構的功能函式
結構的功能函式 極限狀態方程2
極限狀態方程2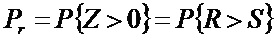 可靠度
可靠度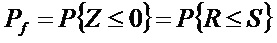 失效機率
失效機率 失效機率和可靠度的互補關係
失效機率和可靠度的互補關係 機率密度函式
機率密度函式 均值
均值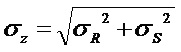 標準差
標準差 結構可靠度
結構可靠度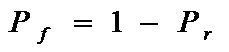 結構失效機率
結構失效機率結構可靠度是在規定的時間和條件下,工程結構完成預定功能的機率,它是工程結構可靠性的機率度量。為了保證結構的安全、適用和經濟,在設計時需要進行結構可靠度分析。....
結構可靠度分析方法(analytical method in reliability of structure)是為了保證工程結構的安全、適用和經濟,在設計時需要進行結構可靠度分析的一種方法。...
在規定的時間和條件下,工程結構完成預定功能的機率,是工程結構可靠性的機率度量。...... 及工程結構材料和構件的質量控制與檢驗方法等,都是工程結構可靠度分析和計算...
《結構可靠度分析——方法與程式》是2009年科學出版社出版的圖書,作者是張明。...... 作為一本結構可靠度分析方法的專著,本書系統介紹了結構可靠度分析的基本概念...
《結構可靠度方法》是2005年同濟大學出版社出版的圖書,作者是(丹麥)迪特萊夫森,(挪威)麥德森。...
《結構機構可靠性及可靠性靈敏度分析》是2017年03月由科學出版社出版發行的一本圖書,作者:呂震宙,宋述芳、李洪雙、袁修開著。...
《工程結構可靠度》是2011年科學出版社有限責任公司出版的圖書。...... 荷載及抗力的統計分析,近似機率法的套用,材料性能的質量要求和控制,以及工程結構可靠度理論發...
《結構可靠性理論與套用》是2008年科學出版社出版的圖書,作者是張偉。...... 本書首先介紹了結構可靠性計算的基本理論,包括結構可靠性計算方法和結構可靠性分析中靈...
基本信息書名結構可靠性設計 書號978-7-118-09461-9 作者芮強 王紅岩 出版時間2014年7月 譯者 版次1版1次 開本16 裝幀精裝 出版基金裝備科技譯著出版基金 ...
《結構可靠性分析與隨機最佳化設計的統一方法》是2015年4月出版的圖書,作者是李洪雙、馬遠卓。...
《結構可靠度分析—方法與程式》是2009年科學出版社出版的圖書,作者是張明。...... 作為一本結構可靠度分析方法的專著,本書系統介紹了結構可靠度分析的基本概念和...
《基於不確定性推理的既有結構可靠性評定》是2011年科學出版社出版的圖書,作者是姚繼濤。...
《水工鋼閘門結構可靠度分析》是2008年中國水利水電出版社出版的圖書,作者是周建方、李典慶。本書主要內容包括鋼閘門結構加固後的可靠度分析、水工鋼閘門面板可靠度...
《高新科技譯叢:結構可靠性設計》介紹了隨著現代結構對關鍵和複雜設計需求的增加,越來越需要一種能夠精確評估廣泛存在於結構系統載荷、幾何、材料性能、加工過程以及...
