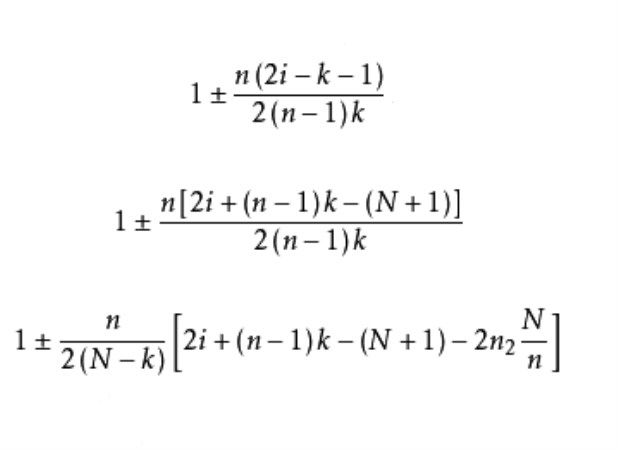等距抽樣二端修正法

基本介紹

設N為總體單位數，n為樣本容量，抽樣間距k=N/n，等距抽樣時在1-k中隨機抽取i作為起點，依次的樣本單位序號為i，i+k，i+2k，…，i+(n-1)k。隨著i的位置偏高或偏低會給估計值帶來偏倚。耶茨(F.Yates)1948年提出了兩端修正法，即對樣本中所有中間單位的權都取為1，而對頭一個和末一個單位給予不同的權：

加號(+)用於頭一個樣本單位，減號(-)用於末一個樣本單位。可以證明，對於任意的i，這兩個權之和為2；當總體為線性趨勢時，加權的樣本均值就是總體均值。

貝爾豪斯(D. R.Bellhouse)與拉奧(J.N.K.Rao)1975年將耶茨的方法推廣到N≠nk時的循環等距抽樣。與耶茨方法一樣，按總體原有次序排列時樣本中的第一個單位與末一個單位給予與1不同的權：此時有兩種情況，一種情況是當i+(n-1)k≤N時(第一個單位取加號，末一個單位取減號) 的權是：

另一種情況是當i+ (n-1) k＞N時的權為：

其中n₂是循環等距抽樣時超過第Y_N個單位的樣本單位的個數。

詳細介紹

處理有線性趨勢的總體的方法

存線上性趨勢時，等距抽樣的效率可以用幾種方法來改進。一是用中心位置的樣本。另一種是將不加權的均值估計量變成加權的，加權時樣本中所有中間單位的權都是1(在除n以前)，但對頭一個和末一個單位給不同的權。若在1到k中抽到的隨機數是i，則這些權就是

加號用於頭一個樣本單位，減號用於末一個樣本單位。對任意i，這兩個權之和是2。讀者可以證明，若總體是由一個線性趨勢所構成的，N=nk，則加權的樣本均值就是準確的總體均值。這些兩端修正方法的效率已由提出方法的耶茨(1948年)驗證過。

貝爾豪斯(Bellhouse)與拉奧(1975年)將耶茨的方法推廣到N≠nk，等距樣本用拉希里的圓形法來抽取的情形，它保證n是常數。和前面一樣，按總體原有次序排列時樣本中的第一個單位與末一個單位給以與1不同的權。例如N=23，n=5時，若抽得起始的一個隨機數是19，於是編號為19，1，6，11，16的單位就組成樣本，第一個和末一個單位是y₁和y₁₉。會出現兩種情況：

情況1 小的i，

，於是所得的n個單位不經過y_N。對第一個單位(+)和末一個單位(-)的權是

情況2i+(n-1)k＞N，設過y_N後所得的樣本單位有n₂個，因此當i=19時，n₂=4。頭一個單位和末一個單位的權是

在這兩種情況下，整個樣本中間的那些樣本單位的權都是1。當

時，頭一個與末一個的權是

。因此y₁的權是11/18，y₁₉的權是25/18。

另外兩種方法是想改變樣本的抽法使得樣本均值不受趨勢的影響。當N=nk，n是偶數時，塞蒂(Seth;1965年)提出的一個方法是把總體分為n/2層，每層含量為2k，在每層中選與兩端等距的兩個單位。當起始的隨機數是i時，n/2對單位的號碼是

等距抽樣二端修正法

基本介紹

基本介紹

詳細介紹

熱門詞條