等距共軛點

任意三角形ABC及平面上一點P，連AP、BP、CP分別交BC、AC、AB於點D、E、F，在邊BC、AC、AB上分別取點D'、E'、F'使得BD'=CD CE'=AE AF'=BF 則AD' BE' CF'三線交於一點Q，則稱Q與P互為等距共軛點。

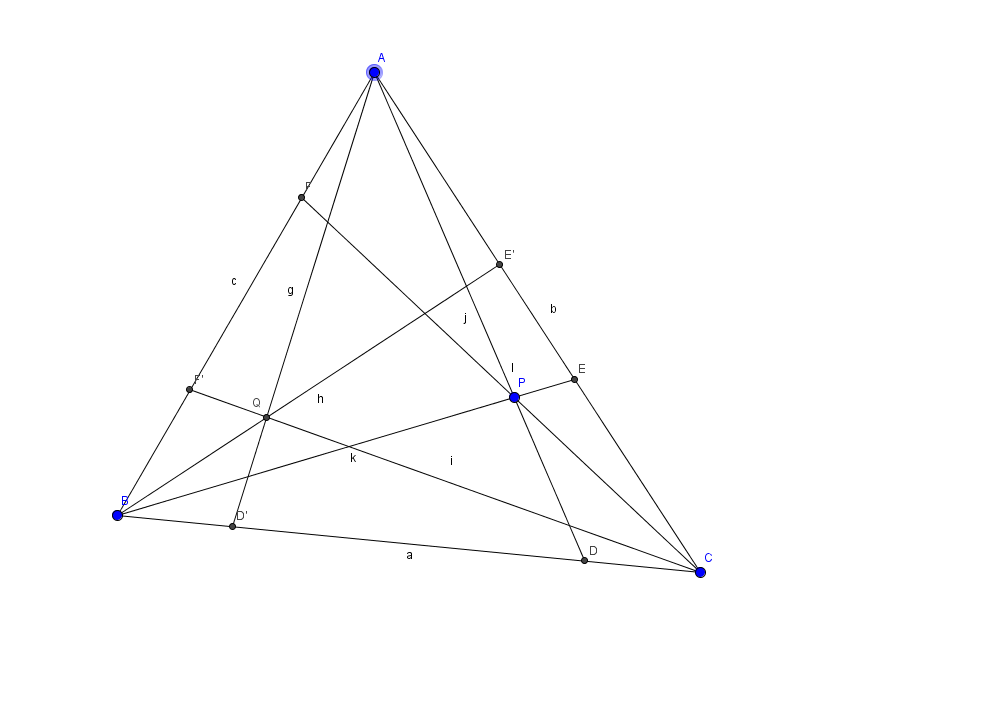
三線共點的證明：

BD'/D'C*CE'/E'A*AF'/F'B=BD/DC*CE/EA*AF/FB

由Ceva定理AD',BE',CF'三線共點。