積分檢驗法

積分檢驗法是汽液平衡數據熱力學一致性檢驗的一種較常用的方法，由於實驗測定汽液平衡數據時往往控制在等溫或等壓條件下，故汽液平衡數據的一致性檢驗也分為等溫和等壓兩種情況。積分檢驗法簡單易行，但是這種方法是對實驗數據進行的整體檢驗而不是逐點檢驗，這樣可能會導致，不同實驗點的誤差可能會相互抵消，而使得面積法通過，因此，通常來說，若不能經過積分檢驗法，則可以說這些實驗數據基本上就是不可靠的，但是通過積分檢驗法的實驗數據也不一定是完全可靠的。若要更為嚴謹的話，可以採用微分檢驗法。

基本介紹

• 中文名：積分檢驗法
• 外文名：Integral test
• 別名：面積檢驗法
• 功能：汽液平衡數據的熱力學一致性檢驗
• 改進方法：微分檢驗法
• 套用學科：化工熱力學

簡介

實驗測定完整的T、p、x、y汽液平衡數據時，產生的測定誤差可能是多方面的，在一定程度上也是不可完全避免的，這就要求測定者和使用者都要判斷所測各組汽液平衡數據的可靠性。從熱力學的角度分析，任一物系的T、p、x、y之間都不是完全獨立的，它們受相律的制約。活度係數是最便於聯繫T、p、x、y值的，採用Gibbs-Duhem方程的活度係數形式來檢驗實驗數據的質量的方法，這種方法稱為汽液平衡數據的熱力學一致性檢驗，積分檢驗法便是常用的一種方法。

等溫汽液平衡數據

理論計算

對於二元系統，其相應的Gibbs-Duhem方程形式為：

在等溫條件下，上市右端第一項為零，對於液相，的數值很小，近似可以取為零，此時上面的式子可寫為：

上式兩邊同時除以dx1，得：

所存在問題

用Gibbs-Duhem方程判斷汽液平衡數據質量時，原則上可以使用上式，但由於導數式涉及不易測準的斜率，所以很難直接使用上式。

改進的計算

赫林頓（Herington）在1947年提出了積分法，由到對式子

進行積分，得到：

最終，可利用上式進行熱力學一致性檢驗，可以標示在積分檢驗曲線上。

積分檢驗曲線

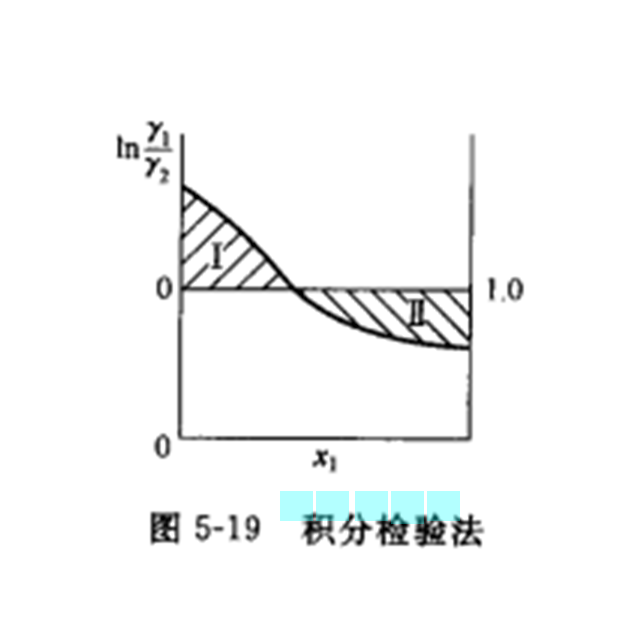
積分檢驗曲線（如圖1所示）與橫坐標所包含面積的代數和應該等於零，即橫坐標以上的面積應該等於橫坐標以下的面積，故此方法又稱為面積檢驗法。由於實驗數據總難免有一定的誤差，實驗值的積分嚴格等於零是不可能的，允許的誤差常視為混合物的非理想性和所要求的精度而定，定義式為：D=|((面積+)-(面積-))/((面積+)+(面積-))|×100，對於具有中等非理想性的系統，當D<2時，可以認為符合熱力學一致性。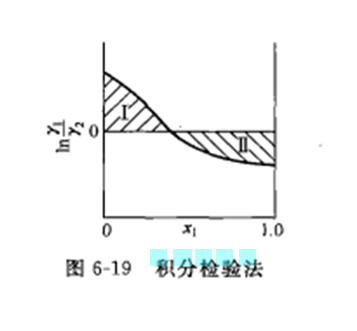

圖1積分檢驗法

等壓汽液平衡數據

在等壓條件下，二元系統相應的Gibbs-Duhem方程右端第二項為零，變為：

由到對上式進行積分，得：

上式的右側常常不可以忽略，其數據又隨著組成而改變，並且較不易獲得，常採用Herington推薦的半經驗方法對二元的等壓汽液平衡數據進行熱力學一致性檢驗，其方法為：由實驗數據得到積分檢驗曲線，並計算出偏差值D，另外，定義：

上式中，分別是系統溫度的最大值的和小值。若(D-J)<10，則認為該套實驗數據符合熱力學一致性。

特點

面積檢驗法簡單易行，但該法是對實驗數據進行整體檢驗而非逐點檢驗。這樣，不同實驗點的誤差可能相互抵消而使面積法得以通過。因此，一般來說，通不過面積法的實驗數據基本上是不可靠的，而通過了面積法的實驗數據也不一定是完全可靠的。

改進方法

若要剔出實驗中的“壞”點，顯然還需要對實驗點進行逐點檢驗，這就要採用微分檢驗法（點檢驗法）。