基本介紹
- 中文名:秤動點
- 外文名:libration point
簡介,位置,L1,L2,L3,L4,L5,平衡性,
簡介
天體系統運動方程的一種靜態特解。當一質點置於該點且初始速度為零,它將在該點保持靜止。
位置
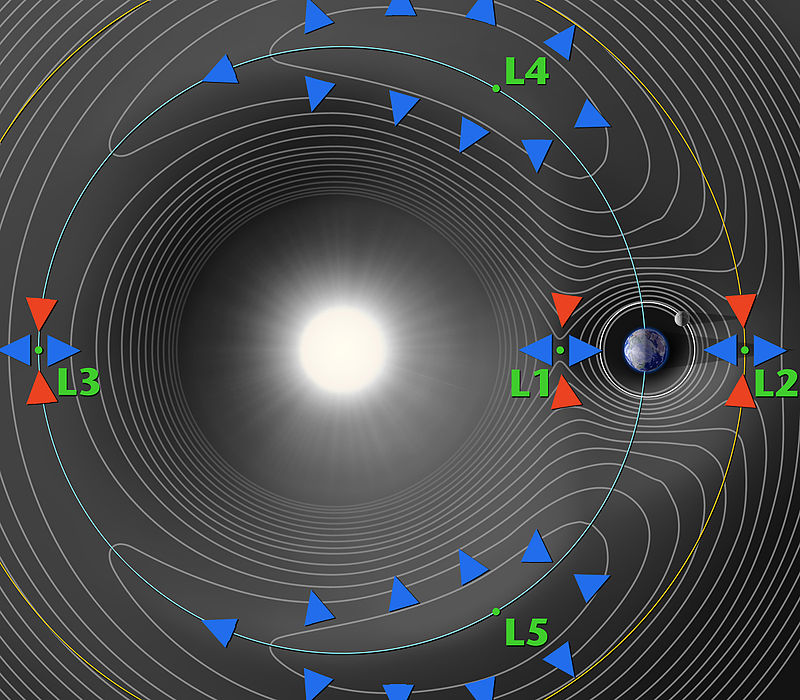
五個拉格朗日點之定義及位置如下:
L1
在M1和M2兩個大天體的連線上,且在它們之間。
- {\displaystyle {\frac {M_{1}}{\left(R-r\right)^{2}}}={\frac {M_{2}}{r^{2}}}+{\frac {M_{1}}{R^{2}}}-{\frac {r\left(M_{1}+M_{2}\right)}{R^{3}}}}
其中:r表示 L1與較小的物體之間的距離,R表示兩個主要物體之間的距離,M1和M2分別表示較大物體和較小物體的質量。
- {\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}
例如一個圍繞太陽旋轉的物體,它距太陽的距離越近,它的軌道周期就越短。但是這忽略地球的萬有引力對其產生的拉力的影響。如果這個物體在地球與太陽之間,地球引力的影響會減弱太陽對這物體的拉力,因此增加這個物體的軌道周期。物體距地球越近,這種影響就越大。在L1點,物體的軌道周期恰好等於地球的軌道周期。太陽及日光層探測儀(SOHO)即在日-地系統的L1點上運行。
L2
在兩個大天體的連線上,且在較小的天體一側。
- {\displaystyle {\frac {M_{1}}{\left(R+r\right)^{2}}}+{\frac {M_{2}}{r^{2}}}={\frac {M_{1}}{R^{2}}}+{\frac {r\left(M_{1}+M_{2}\right)}{R^{3}}}}
同樣的,當小物體的質量(M2)遠小於大物體的質量(M1)時:
- {\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}
日地系統的L2在地球遠離太陽的一側。一般來講,一個物體距太陽的距離越遠,它的軌道周期通常就越長,但L2點上的物體還受到地球的引力,所以軌道周期變得與地球的相等。日地系統的L2通常用於放置空間天文台。因為L2上的物體可以保持背向太陽和地球的方位,易於保護和校準。威爾金森微波各向異性探測器已經在日-地系統的L2點上運行。詹姆斯韋伯太空望遠鏡將要被放置在日-地系統的L2點上。嫦娥二號台北時間2011年8月25日23時27分,經過77天的飛行,“嫦娥二號”在世界上首次實現從月球軌道出發,受控準確進入距離地球約150萬公里遠的、太陽與地球引力平衡點——拉格朗日L2點的環繞軌道。
地月系統的L2在月球遠離地球的一側(月球背面)。2014年中國探月工程三期再入返回飛行試驗器服務艙曾進入環繞地月L2點的李薩如軌道開展試驗。服務艙實現了環繞地月L2點飛行三圈,驗證了軌道設計、軌道控制和軌道維持技術。
L3
在兩個大天體的連線上,且在較大的天體一側。
- 例如:第三個拉格朗日點,L3,位於太陽的另一側,與太陽的距離略小於地球與太陽的距離,但是位於地球軌道的外部,這個看上去矛盾的表述是因為地球公轉軌道的焦點,是太陽與地球的共同質心,儘管對於日地系統來說共同質心在太陽內部,太陽同時也在圍繞這個共同質心轉動,所以這種狀態成為可能。
L4
在以兩天體連線為底的等邊三角形的第三個頂點上,且在較小天體圍繞兩天體系統質心運行軌道的前方。此點穩定的原因在於,它到兩大物體的距離相等,其對兩物體分別的引力之比,正好等於兩大物體的質量之比。因此,兩個引力的合力正好指向該系統的質心,合力大小正好提供該物體公轉所需之向心力,使其旋轉周期與質量較小天體相同並達成軌道平衡。該系統中,兩大物體和L4點上物體圍繞質心旋轉,旋轉中心與質心重合。事實上,L4和L5點上的物體的質量不須小到可忽略。L4和L5點處,小物體受太陽和地球的引力的合力指向日地共同質心且大小正合適。
L5
在以兩天體連線為底的等邊三角形的第三個頂點上,且在較小天體圍繞兩天體系統質心運行軌道的後方。
L4和L5有時稱為三角拉格朗日點或特洛伊點。科幻作品(如漫畫、小說)所說的用於放置殖民衛星的拉格朗日點特指L4和L5,不包括L1和L2。
- 例如:L4和L5在地球圍太陽運行的軌道之前和之後成60°角處。
實質上是三個物體圍繞共同質心轉動。
平衡性
嚴格而言,首先拉格朗日點只算是二星體連線之法平面內的穩定點,而在三維空間內則不穩定:考慮L1:若垂直於中線地推移測試質點,則有一力將其推回平衡點(穩定平衡);但若測試質點漂向任一星體,則該星體之引力會將其拉向自己(不穩定平衡)。L1、L2和L3點在這條直線上不穩定,如果把物體放在這上面的話,它馬上會離開這個點。所以,有一種軌道的設計就是,它是圍繞L2點做周期運動(Halo orbit),這樣的話,我們的衛星只需少量調節便能維持其軌道。
此對比:若M1比M2大於24.96,則處於L4與L5的物體是穩定平衡:當一測試質點偏離此平衡點,則科里奧利力會將其軌道扭曲成(相對於旋轉座標之)扁豆狀。太陽-木星系統有幾千枚小行星,通稱為“特洛伊小行星”,俱劃此等軌跡。太陽-火星、太陽-土星、木星-木衛、土星-土衛等系統亦有類似星體。日-地系統中亦有2010 TK7(第一顆地球特洛伊小行星),在二十世紀五十年代發現塵霧圍繞L4與L5。在地-月系統之L4與L5點亦發現比對日照更微弱之塵霧。
地球的伴星(companion object)克魯特尼以類似特洛伊之軌道“圍繞”地球,但不是真正的特洛伊衛星,它基本上以一周期略小於一年之橢圓軌道環繞太陽,接近地球時從地球公轉提取動能而進入較高之軌道。當克魯特尼被地球追上,則會交回此動能,跌落低能軌道,重新開始循環。