發現
這個現象的早期描述由
托馬斯·楊在1800年給皇家學會的演講中提供:
將來自吹氣管的蠟燭的火焰推向空氣流的橫向壓力可能與減輕靠近障礙物的空氣流的拐點的壓力完全相似。標記一個細長的空氣流在水面上的凹坑。將凸體與流體的一側接觸,凹坑的位置將立即顯示電流朝向身體偏轉;如果身體在每個方向都能自由移動,就會被迫朝當前的方向發展。
一百年後,亨利·科蘭迪(HenriCoandă)在實驗中發現了他的Coandă-1910飛機的套用,這架飛機設計了一種不尋常的引擎。電動渦輪機向後推動熱空氣,Coandă注意到氣流被吸引到附近的表面。在1934年,Coandă在法國獲得了一項“將流體轉移到另一種流體中的方法和裝置”的專利。該效果被描述為“在凸壁附近滲透另一種流體的流體的平均射流的偏差”。明確提及Coandă效應的第一份正式檔案是HenriCoandă的兩項1936年專利,這個名字被領先的空氣動力學家西奧多·馮·卡爾曼(西奧多·馮·卡爾曼)接受,他與科安達在空氣動力學問題上有著悠久的科學關係。
康達作用機制
空氣流將從周圍的周圍引入空氣分子,造成射流周圍的低壓“管”或“套筒”。來自這個低壓管周圍的環境空氣將對射流施加一個力,當從橫截面看時,其在所有方向上是相等的。因此,噴氣機不會偏離直線移動。然而,如果固體表面靠近噴嘴放置並近似平行,則空氣從固體表面和噴嘴之間的夾帶(並因此去除)會導致減少不能像射流“敞開”一側的低壓區域那樣快速中和的射流那邊的空氣壓力。橫穿射流的壓力差導致射流偏離附近的表面,然後粘附到其上。即使它是彎曲的,射流也將粘附到表面上,因為每個(無窮小的)增量的表面方向上的變化會帶來噴射朝向表面的初始彎曲所描述的效果,如果表面不是太尖銳地彎曲,則在適當的情況下,即使在圓柱形彎曲表面上流動180°之後,射流也可以附著在表面上,因此在與其初始方向相反的方向上行進。引起噴射流動方向的這些變化的力在噴流流動的表面上產生相等且相反的力。這些Coandă效應誘發的力可以被利用來引起升力和其他形式的運動,這取決於射流和射流附著的表面的取向。
在噴嘴開始流過該表面的點處的表面上的小的“唇”(參見圖1)增強了射流的流動方向的初始偏差,並且隨後的附著表面。這是由於低壓渦流形成在唇緣後面,促使射流向表面的傾斜。
Coandă效應可以在任何流體中誘導,因此在水中與空氣中同樣有效。
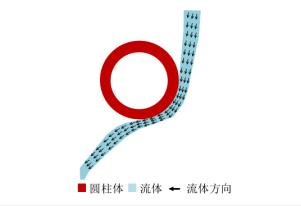 圖1 Coandă效應
圖1 Coandă效應存在條件
早期資料提供了理論和實驗兩方面的信息,需要通過比較得出Coandă效應及其限制的詳細解釋。可以在自由射流或壁射流中沿彎曲的壁發生共同作用。
“康達效應的機制”,以T.Young的術語所描述的“減輕障礙物附近的空氣的電流的側向壓力”的效果表示從噴口出來的自由噴嘴和周圍的障礙物。它包括從孔口出來的自由射流的趨勢,以限制進入的環境夾帶流體,而在周圍沒有障礙物的情況下,不會發展出任何較低壓力的區域,如在湍流混合發生在環境壓力下。
在正確的圖像上,效果沿著彎曲的牆壁發生作為壁射流。在兩個平行的平面壁之間的二維壁噴射,其中“障礙物”是遵循扁平的水平矩形孔的四分之一圓柱形部分,使得根本沒有流體從周圍沿壁被夾帶,但僅在與環境空氣湍流混合的相對側。
為了比較理論模型的經驗,我們首先參考半徑為r的圓形壁的寬度為h的二維平面壁射流。牆壁射流遵循無窮大半徑的平坦的水平牆壁,或者其半徑是地球的半徑而沒有分離,因為混合區域中的表面壓力以及外部壓力均等於大氣壓力和邊界層不與牆分離。沿半徑r = 12cm的圓形彎曲壁測量表面壓力,使寬度為h的湍流空氣(雷諾數= 106)偏轉。由於在噴嘴出口處的局部效應,噴射頭的起始點之前,壓力開始下降,從而產生射流。如果h / r比(射流的寬度與壁的曲率半徑的比率)小於0.5,則觀察到真實的Coandă效應,沿著彎曲壁的壁壓力保持在該低(亞環境壓力)水平,直到射流到達壁的端部(當壓力迅速恢復到環境壓力時)。如果h / r比大於0.5,則只有局部效應發生在射流的起點,之後噴射立即與牆壁分離,並且沒有Coandă效應。
在1956年,以各種噴射寬度(h)的雷諾數為106的湍流空氣射流進行的實驗顯示沿著與射流原點一系列水平距離的圓形彎曲壁(半徑r)測量的壓力。
在0.5以上的臨界h / r比之下,只有沿射流原點的局部效應才能沿彎曲的壁18°的小角度延伸。噴氣機立即與彎曲的牆壁分離。因此,這裡沒有看到Coandă效應,而僅僅是局部附屬檔案:在壁上出現的壓力小於對應於9°的小角度的距離,隨後是等於9°的角度,其中該壓力增加到在邊界層分離時的大氣壓力,受到這種正的縱向梯度。然而,如果h / r比值小於0.5的臨界值,則在噴氣發生器上觀察到的壁上測量的環境壓力低於牆壁。這是一種真正的Coandă效應,因為射流以幾乎恆定的壓力附著在牆上“,如在傳統的壁射流中。
LC Woods在1954年對圓形壁的非粘性流程進行的計算表明,存在任何曲率h / r和任何給定的偏轉角直到壁上的分離點的無粘性解,其中出現奇異點具有表面壓力曲線的無限斜率。
在計算中,對於每個相對曲率h / r的值,在前述實驗中發現的分離角度,最近獲得了這裡的圖像,並顯示了由非粘性解決方案表示的慣性效應。
套用
空氣動力
附壁作用是大部分飛機機翼的主要運作原理。
附壁作用的突然消失是飛機
失速的主要原因。部分飛機特別使用引擎吹出的氣流來增加附壁作用,用以提高升力。美國
波音的YC-14及
前蘇聯的安-72都是把噴射發動機裝在機翼上方的前面,配合襟翼,吹出的氣流可以提高低速時機翼的升力。波音的
C-17運輸機亦有透過附壁作用增加升力,但所產生的升力較少。直升機的「無尾螺旋」(NOTAR) 技術,亦是透過吹出空氣在機尾引起
附壁作用,造成推力平衡旋翼的作用力。
 康達效應
康達效應利用 Coanda 效應,可以有意識地誘導空氣氣流,在機翼上表面產生比飛機和空氣相對速度更大的氣流速度,提高升力。70 年代時,美國空軍已經意識到
C-130在速度、航程和載重上的局限,希望用噴氣式中型戰術運輸機取代,這就是“先進中型短距起落運輸機”(Advanced Medium STOL Transport)計畫的由來。經過60年代的無功而返,美國空軍已經不再強調
垂直起落,所以AMST只要求短距起落。波音和
麥道的AMST方案分別入選,參加對比試飛。波音的方案YC-14利用Coanda效應,發動機置於機翼前緣上方,噴流直接吹拂由於襟翼放下而彎度大增的機翼上表面,不光直接產生Coanda效應,還誘導周邊的氣流,一同產生增升效果。YC-14的試飛是成功的,但這時國防部採購政策正在助理國防部長David Packard 手裡大刀闊斧地改革,AMST計畫最終被取消了。波音YC-14的“上表面吹氣增升”(Upper Surface Blowing,簡稱USB)最終
牆裡開花牆外香,被
安東諾夫用到安-72 上,後者成為第一架採用USB的量產型飛機。
飛碟設計
不過 Coanda 效應不是只能用於
短距起落飛機的。用好了,Coanda 效應可以實現垂直起落,這其中的佼佼者就是加拿大Avro 的 Avrocar。關於飛碟的傳說很多,最後大多被證明只是人們的想像,但 Avrocar 確實很像飛碟,這大概是最接近傳奇式的飛碟的飛行器了。Avrocar 就像一個上面圓渾的大碟子,中間是進氣的圓孔,周邊是一圈小噴嘴。發動機產生高壓排氣,通過周邊的噴嘴噴出,拉動上方氣流,沿上表面高速從中心向周邊流動,在飛行器靜止的時候就可以形成升力,達到垂直起飛。垂直起飛後,重新調整周邊噴嘴的氣流分布,就可以實現噴氣推進,一旦達到一定速度,飛碟本身的形狀就可以產生氣動升力,這時轉入正常飛行。Avrocar 是美國陸軍 VZ 系列垂直起落研究機中的一個,在試飛中演示了垂直起落能力,但無法飛出
地效高度,一進入無地效飛行,飛行控制就顯得力不從心,飛行穩定性沒法解決,最後下馬了,留下一段
飛碟的佳話。
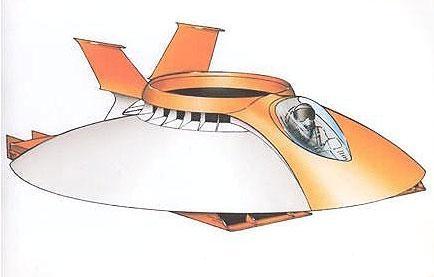 柯恩達效應飛行器
柯恩達效應飛行器升力的成因
然而當今有部分學者認為機翼產生升力的原理就是因為康達效應,即機翼把大量氣流向下偏轉而產生一個反作用力(升力)。這樣的理解並不完全正確,真實環境下的飛機
升力有多重因素,主要還是因為機翼上下表面壓力差。另外,在超聲速飛行時,反作用力仍存在,不過不占大比重。
實驗演示
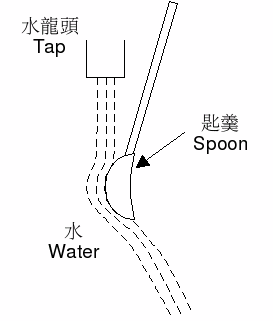
打開
水龍頭,放出小小的水流。把小
湯匙的背放在流動的旁邊。水流會被吸引,流到湯匙的背上。這是
附壁作用及
文丘里效應(Venturi Effect)作用的結果。當水流附在湯匙上以後,附壁作用令水流一直在湯匙上的凸出表面流動。
這個實驗就是水流對物體施與
反作用力的典型例子,然而不少觀點認為湯勺被吸附是因為伯努利原理,導致水流過的一部分流速加快,壓力變小,另一部分沒有水流,壓力較大。顯然這種說法十分荒唐,伯努利原理不可用於物體處於兩種不同流體間的比較,湯勺正面受到
大氣壓,背面也受到大氣壓,儘管水流通過但不影響壓力大小。一個反例就是,當你把勺子正面對著水流,就是讓水流流過向內凹的一面,可以清楚地看到勺子朝遠離水流的方向偏轉了。
 圖1 Coandă效應
圖1 Coandă效應 康達效應
康達效應 柯恩達效應飛行器
柯恩達效應飛行器
