社團結構

近年來對眾多實際網路的研究發現,它們存在一個共同的特徵,稱之為網路中的社團結構。它是指網路中的頂點可以分成組,組內頂點間的連線比較稠密,組間頂點的連線比較稀疏。

基本介紹

• 中文名：社團結構

定義

關於網路中的社團結構目前還沒有被廣泛認可的唯一的定義,較為常用的是基於相對連線頻數的定義:網路中的頂點可以分成組,組內連線稠密而組間連線稀疏。這一定義中提到的“稠密”和“稀疏”都沒有明確的判斷標準,所以在探索網路社團結構的過程中不便使用。因此人們試圖給出一些定量化的定義,如提出了強社團和弱社團的定義。強社團的定義為:子圖V中任何一個頂點與y內部頂點連線的度大於其與V外部頂點連線的度。弱社團的定義為:子圖V中所有頂點與V內部頂點的度之和大於V中所有頂點與V外部頂點連線的度之和。此外,還有比強社團更為嚴格的社團定義——LS集,一個LS集是一個由頂點構成的集合,它的任何真子集與該集合內部的連邊都比與該集和外部的連邊多。

另一類定義則是以連通性為標準定義社團,稱之為派系。一個派系是指由3個或3個以上的頂點組成的全連通子圖,即任何兩點之間都直接相連。這是要求最強的一種定義,它可以通過弱化連線條件進行拓展, 形成n-派系。例如:2-派系是指子圖中的任意兩個頂點不必直接相連,但最多通過一個中介點就能夠連通。3-派系是指子圖中的任意兩個頂點,最多通過兩個中介點就能連通。隨著n值的增加,n-派系的要求越來越弱。這種定義允許社團間存在重疊性。所謂重疊性是指單個頂點並非僅僅屬於一個社團,而是可以同時屬於多個社團。社團與社團由這些有重疊歸屬的頂點相連。有重疊的社團結構問題有研究的價值,因為在因為在實際系統中,個體往往同時具有多個群體的屬性。除上述提到的社團定義以外,還有多種其他定義方式,文獻[24]進行了更為詳細的介紹。

社團劃分思路及社團劃分的相關問題

社團劃分思路

照複雜網路中社團形成的過程,網路中社團結構的劃分思路大體可以分成4類:凝聚過程、分裂過程、搜尋過程和其他過程。 凝聚過程是以頂點為基礎,通過逐步凝結形成社團。其主要步驟為:1)設定某種標準可以衡量社團與社團之間的距離或相似度;2)將網路中的每一個頂點視為一個社團,所以網路中有多少頂點就有多少初始社 團,並且每個社團只包含一個頂點;3)根據設定的衡量標準,計算社團與社團間的距離或相似度,並將距離 最近的社團或相似度最高的社團合併在一起形成新的社團;4)重新計算每對社團間的距離或相似度;5)不斷重複合併及重新計算的步驟,直到所有頂點都聚集成一個社團。整個過程可以用一個倒立的樹狀圖表示。

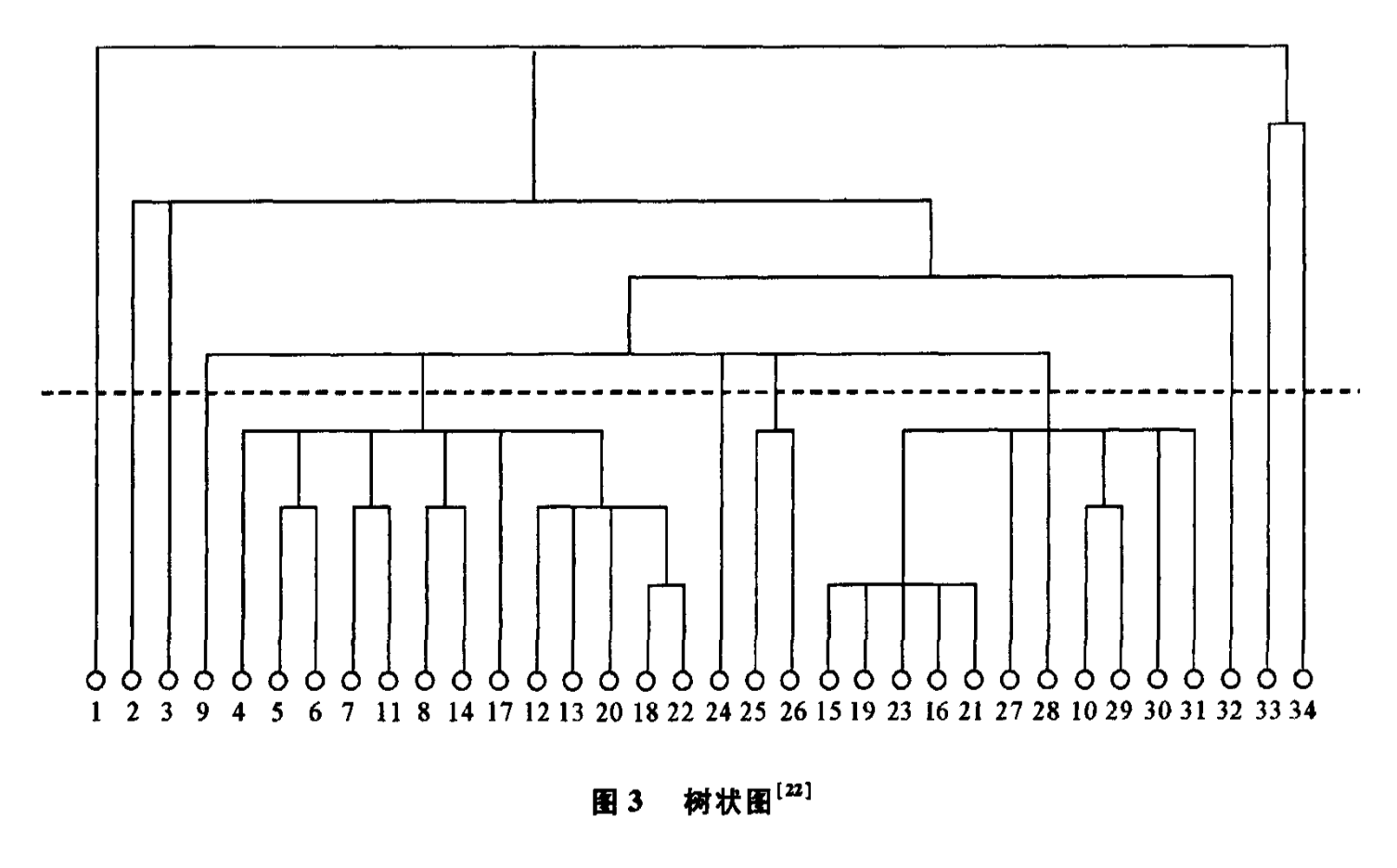樹狀圖

分裂過程則相反,它首先將網路中的所有頂點都視為一大社團,通過逐步分割這個大社團形成小社團。其主要步驟為:1)設定某種衡量頂點間密切程度或邊對網路結構影響程度的指標;2)按照一定標準進行斷 邊;3)不斷重複計算和斷邊的過程,網路將被劃分成一個個越來越小的連通社團,這些連通社團就是對應某一階段的社團;4)全部過程以每個頂點被獨立地分成一個社團為終點。整個過程可以用一個直立的樹狀圖表示,過程方向與凝聚過程相反。

搜尋過程不拘泥於統一的凝結或分裂,而是建立一個逐步最佳化目標的探索過程,社團結構直接由最後的最佳化結果給出。搜尋的方法可以套用成型的算法,Potts模型算法中就套用了模擬退火算法進行搜尋。

劃分方法的複雜度研究

由於各種劃分方法在判斷標準,最佳化思路、搜尋步驟等方面的不同,每種劃分算法都有其自身的複雜度。複雜度往往與被研究網路的頂點數目、邊的數目、層次的數目、社團的數目有關。劃分方法的複雜度越高劃分所需的時間越長。對於較小的網路,劃分方法所需時間的長短不會產生本質的影響。然而由於受到計算機技術的制約,一種劃分方法的複雜度決定該劃分方法能否運用於大規模的網路。可見,算法複雜度既是判斷劃分方法速度的標準,又是判斷劃分方法適用範圍的標準。複雜度越小的劃分方法,劃分的速度越快,適用的網 絡規模越大。因此,構造複雜度低的算法,是科研工作者的目標之一。

檢驗劃分方法的經典網路

檢驗劃分方法的網路有兩大類:人造網和實際網。之所以要構建人造網,是因為人造網的結構可以人為給定,在分析之前就擁有較多的已知信息,從而可以用來檢驗劃分方法的有效性及正確率。另外,人造網的參數可以調控,從而可以研究劃分方法的適用範圍,以及劃分正確率與參數的聯繫。常用的人造網是由128個頂點構成的網路,這128個頂點被平均分成4份,形成4個社團,每個社團包含32個頂點。頂點之間相互獨立的隨機連邊,如果兩頂點屬於一個社團,則以機率P_in相連,如果兩點屬於不同的社團,則以機率P_out相連。P_in和P_out的取值,保證每個頂點的度的期望值為16。記Z_in為頂點與社團內部頂點連邊數目的期望值,Z_out為頂點與社團外頂點連邊數目的期望值,從而Z_in+Z_out=16。Z_out越小,說明頂點與社團外頂點的連邊越少,網路的社團結構越明顯; Z_out越大,說明頂點與社團外頂點的連邊越多,網路越混亂,社團結構越不明顯。對於 Z_out值大的網路還能夠基本正確對網路進行劃分的方法,在實際套用中適用範圍更廣,價值更大。眾多方法的實踐表明,當Z_out的取值在一定範圍內時,其值對頂點劃分正確率沒有影響,並且正確率都保持在100%, 然而當Z_out的取值超過這一臨界值之後,網路中頂點被正確劃分的比率與Z_out的取值呈現負相關關係,即Z_out越大,頂點被正確劃分的比例越低。

人造網的檢驗在一定程度上反映了劃分方法的有效性。然而,由於人們感興趣的問題大多是實際網路, 所以需要用實際網路對劃分方法進行再檢驗。選擇用作檢驗的實際網路時,首先要保證構建網路的數據是方 便易得的;其次要保證網路有實際的意義,從而可以判斷社團劃分的結果是否具有可解釋性;另外為了方便劃分方法間的比較,宜採用已被廣泛使用的實際網路。

空手道俱樂部網:20世紀70年代初,Wayne Zachary觀察了美國大學空手道俱樂部成員間的人際關係,並依據俱樂部成員間平時的交往狀況建立了一個網路。這個網路包含34個頂點,代表了俱樂部成員;包含了78條邊,代表他們之間的人際關係。由於突發的原因,俱樂部管理者與俱樂部主要教師之間針對是否提高收費這一問題產生了激烈的爭論,並最終導致俱樂部分裂成兩部分。圖4為空手道俱樂部網,其中方形頂點代表歸於俱樂部管理者(1號頂點)的成員,圓形頂點代表歸於俱樂部主要教師(33號頂點)的成員。

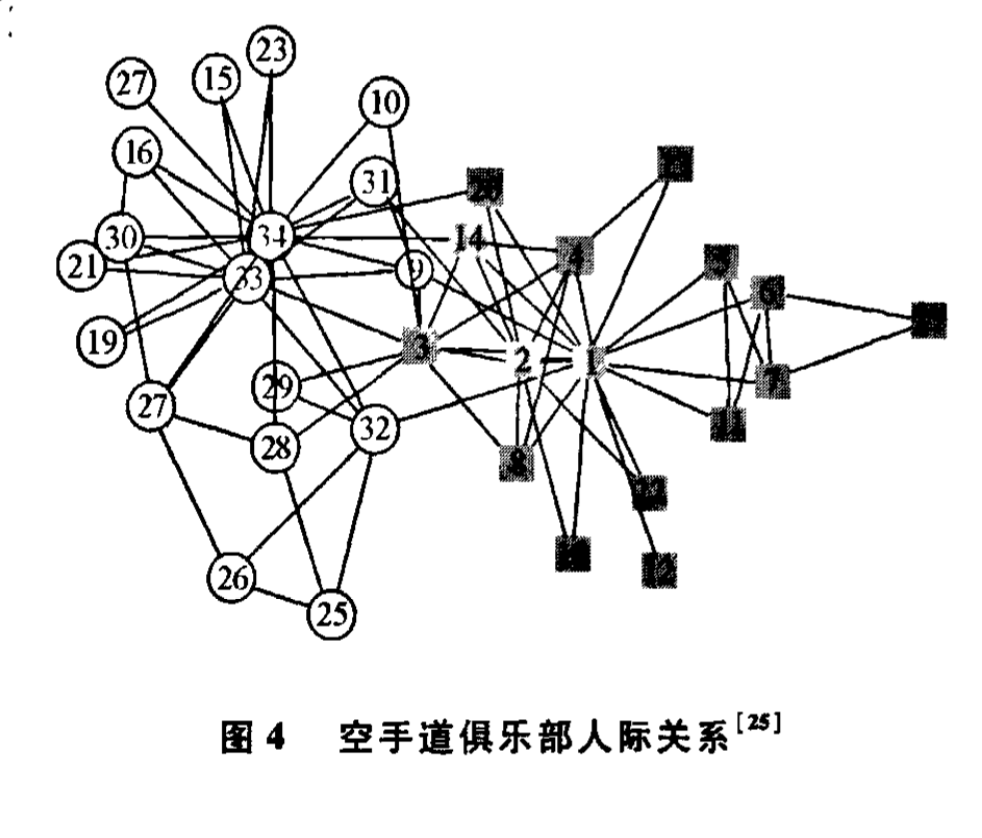空手道俱樂部人際關係

科學家合作網:科學家之間合作的表現方式是廣泛的,如文章的合作、引用、致謝。這裡介紹3個科學家合作網:1)物理學家合作網,它是收集了arxiv.org網上的關注於物理研究的科學家的文章,並據此構建的科學家合作網。其中頂點表示發表過文章的科學家,如果兩位科學家共同發 表過文章就將他們用邊連線起來;2)桑塔菲研究所科學家合作網,是收集了1999年、2000年研究所內271位科學家的合作情況構建的網路,其中的頂點是桑塔菲研究所內的科學家,如果他們合作發表過文章,就將他們用邊連線起來;3)經濟物理學家合作網收集了經濟物理學主頁上發表的文章、Physiea A發表的經濟物理學文章、ISI上發表的文章,根據文章的合作、引用、致謝建立經濟物理學者之間的關係。

類似的還有根據美國大學橄欖球隊2000年一個賽季的賽程建立的網路,其中頂點代表大學的橄欖球隊,共有115支大學橄欖球隊,連邊表示兩隊之間進行了常規賽,這一賽季共包含616場常規賽;根據Linda Wolfe收集的猴子3個月的活動數據,通過猴子之間相互刷毛的關係抽象出的網路舊引,其中16個頂點代表16 只猴子,若兩隻猴子相互刷毛則用邊連線起來,共有69條邊。在這些實際網路中,除了空手道俱樂部網和美國大學橄欖球比賽網有可以判斷劃分準確性的已知社團結構,其他網路並沒有這樣的標準,因此用來判斷劃分方法優劣的標準是劃分結果是否具有可解釋性。雖然這樣的判斷標準是不嚴謹的,然而社團結構劃分的主要對象正是這樣未知結果的網路,因此結果更具解釋性的劃分算法更有價值。

社團劃分的具體算法

隨著關注網路社團結構問題的科研工作者不斷增加,眾多劃分網路社團結構的算法被設計出來。根據不同的標準,這些算法可以被分成不同的種類。例如:根據社團結構的形成過程,算法可以分為凝聚算法、分裂算法,搜尋算法及其他算法4大類。從算法的物理背景上考慮,又可以將其分為基於網路拓撲結構的算法,基於網路動力學的算法,基於Q函式最佳化的算法及其他算法。

研究意義

社團結構在實際系統中有著重要的意義:在人際關係網中,社團可能基於人的職業、年齡等因素形成;在引文網中,不同社團可能代表了不同的研究領域;在全球資訊網中,不同社團可能表示了不同主題的主頁;在新陳代謝網、神經網中,社團可能反映了功能單位;在食物鏈網中,社團可能反映了生態系統中的子系統。在網路性質和功能的研究中,社團結構也有顯著的表現。例如:在網路動力學的研究中,當外加能量處於較低水平時同一社團的個體就能達到同步狀態;在網路演化的研究中,相同社團內的個體可能最終連線在一起。總之,對網路中社團結構的研究是了解整個網路結構和功能的重要途徑。

複雜網路社團結構分析在實際問題中還沒有得到廣泛的套用,僅僅涉及Intemet網、科學家合作網等領域,但其在大腦系統、生物系統、經濟系統、管理系統等領域的套用可能會揭示出以往方法未發掘的信息。不僅如此,網路社團結構對實際問題還有著指導意義。因此,社團結構對分析解決實際問題的價值需要進一步的探討。