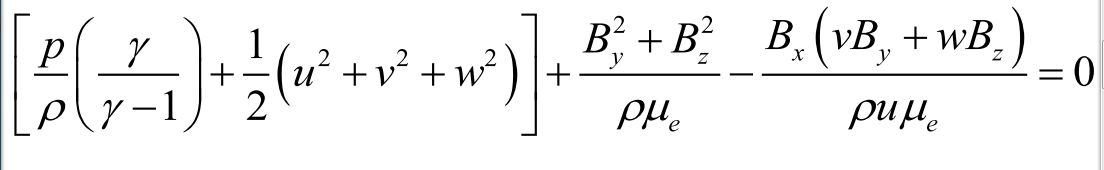磁流體動力學波（Magnetohydrodynamics）導電流體（例如電漿或液態金屬）在頻率遠低於離子迴旋頻率的強磁場中的波動，是研究電漿和磁場的相互作用的物理學分支，其基本思想是在運動的導電流體中，磁場能夠感應出電流。磁流體力學將電漿作為連續介質處理，要求其特徵尺度遠遠大於粒子的平均自由程、特徵時間遠遠大於粒子的平均碰撞時間，不需考慮單個粒子的運動。由於磁流體力學只關心流體元的平均效果，因此是一種近似描述的方法，能夠解釋電漿中的大多數現象，廣泛套用於電漿物理學的研究。更精確的描述方法是考慮粒子速度分布函式的動理學理論。磁流體力學的基本方程是流體力學中的納維-斯托克斯方程和電動力學中的麥克斯韋方程組。磁流體力學是由瑞典物理學家漢尼斯·阿爾文創立的，阿爾文因此獲得1970年的諾貝爾物理學獎。
概述,阿爾文波,磁流體小振幅波,磁流體激波,參考書目,
概述
磁流體動力學波的發現同宇宙電動力學的理論研究有關。1942年，H.阿爾文首先發現一種磁流體動力學波(後稱為阿爾文波)，並用它解釋太陽黑子現象。另外，如磁聲波等也屬於磁流體動力學波。許多學者對這個問題作了大量的理論和實驗研究。若導電流體採用單流體模型，則小振幅的和有限振幅的磁流體動力學波都可分為熵波、阿爾文波、慢磁聲波和快磁聲波。此外，在導電流體中還可以傳播一些間斷面，包括切向間斷、接觸間斷、旋轉間斷（阿爾文間斷）和磁流體激波。如果導電流體採用多組元模型，磁流體動力學波的種類就更豐富。下面分別就阿爾文波、磁流體小振幅波和磁流體激波作簡要說明。
阿爾文波
阿爾文波的存在已在實驗中得到證實。實驗方法大多是把裝有導電液體（如水銀、液態鈉等）的專用容器浸沒在已知強度的磁場中，然後設法使導電液體中產生周期擾動。通過測定擾動傳播的時間即可求得擾動速度。阿爾文波速度有非常寬的範圍。在使用水銀的實驗中，當B0=0.1特時,vA是1米/秒量級。在太陽光球的高磁場區，如果發生波動，由於密度低，vA接近於聲速。
磁流體小振幅波
導電流體中的電磁力和慣性力具有可以比較的數量級。設一個均勻定常磁場B0充滿整個空間，而擾動以波的形式傳播。假定未受擾動的導電流體是靜止的，擾動後隨著導電流體的波動會產生壓力、密度、溫度、速度和磁場的小振幅擾動。由於磁力線隨導電流體一起運動而產生的恢復力以多種不同形式同流體壓力相結合，因而產生多種多樣的波的模式。如果忽略所有耗散，即考慮一種無粘性、無熱導和具有無限電導率的理想導電流體，則存在四類波：熵波、快磁聲波、慢磁聲波和斜阿爾文波。考慮兩種特殊情況，即波的傳播方向和磁場的方向或者相同，或者垂直。相同時，斜阿爾文波的波速是vA，而慢磁聲波和快磁聲波中的一個波速是聲速，另一個波速是vA；垂直時，僅有快磁聲波。這個結論僅適用於低頻情況，即波的頻率ω遠小於離子迴旋頻率Ωi=eB0/mi，式中e和mi分別為離子的電荷和質量。當頻率增加時,相速度會發生明顯變化。熵波的相速度就是電漿的當地速度。上述的磁流體動力學波屬於熱電漿的低頻模式。這些模式忽略了位移電流。
當波的相速度遠大於電子和離子的熱運動速度時，即使是相當熱的電漿，還是可以近似用所謂冷電漿的模型來描述。在這種情況下，忽略電子和離子的熱運動速度意味著忽略流體的壓力和溫度，同時必須計及位移電流的影響。冷電漿波的傳播方向K的兩種特殊情形如下：
①K∥B0 有兩種波：右旋波和左旋波。兩者都是圓偏振的，它們的電場E都是旋轉的（見圖）。右旋波的E的旋轉方向和K構成右手螺旋，因此E的旋轉方向和電子繞B0的旋轉方向相同。左旋波的E的旋轉方向和K構成左手螺旋，因此E的旋轉方向和離子繞B0的旋轉方向相同。ω《Ωi(極低頻)時的左旋波稱為剪下阿爾文波；ω<Ωi時的左旋波稱為離子迴旋波；當ω →Ωi時，波和離子發生共振。
圖1 右旋波R和左旋波L
此外，還可有ω=ωp=(ne/ε0me),式中n、me和e分別為電子的數密度、電子質量和電子電荷；ε0為真空電容率。這是一種電漿振盪模式，振盪僅以電子電漿頻率ωp進行，而且在冷電漿模型下振盪不傳播（見電漿振盪）。
②K⊥B0 有兩種波：尋常波和非常波。尋常波的電場E和B0平行,是電漿中的光波；非常波的E和B0垂直。ω《Ωi(極低頻)時的非常波稱為壓縮的阿爾文波或磁聲波，它的波速和剪下阿爾文波的波速相同。剪下阿爾文波從電動力學和力學方面看來都是橫波，而壓縮的阿爾文波，從電動力學方面看來是橫波，但從力學方面看來可近似地視為縱波。當ω →Ωi時,壓縮的阿爾文波的特性不發生根本變化,它不僅在低於或稍高於Ωi時傳播，就是在離子迴旋共振即ω=Ωi時仍然可以傳播。
磁流體激波
在磁流體力學中，如同在普通流體力學中一樣，對於有限振幅波的傳播速度，要根據狀態變數的局部值和磁場強度來計算。在不同點上，波的傳播速度一般是不相同的。因而，磁流體力學波傳播時，波形發生變化，波陣面逐漸變陡，最後發展成為物理狀態急劇變化的薄層──激波。根據磁場方向與波陣面法線方向的方位不同，磁流體激波可區分成正激波和斜激波，而正激波則是斜激波的特殊情況。
磁流體激波理論比普通流體的激波理論複雜得多。在磁流體激波中，除了考慮密度、溫度等以外，還必須考慮磁場的變化，因此，在磁流體力學中會出現更多的激波類型。研究磁流體激波最有用和最簡單的方法是把激波過渡區近似地當作流體參量的間斷面，而通過間斷面的流體參量仍須遵循物理守恆定律。 假設激波沿x方向運動，並設坐標隨激波一起運動,取激波面為y-z平面，用[φ]表示物理量嗞在激波前後的差值φ2－φ1,其中下標1表示激波前的物理量，下標2表示激波後的物理量,則對於具有無限電導率的理想氣體的激波，有下列關係：
連續性方程
動量方程：
磁傳輸方程：
能量方程：
式中u、v、ω分別為流體速度在x、y、z軸上的分量;Bx、By、Bz分別為磁場B在x、y、z軸上的分量；p為流體壓強；ρ為流體密度；μe為磁導率；γ為比熱比。這些方程有時稱為橫越激波的跳躍條件。通常激波前的流體狀態為已知，如果激波速度已知或者已經測得，則激波後的物理量即能確定。
如果Bx=0，則成為磁流體力學正激波。正激波前後的磁場都平行於激波面。速度矢量可以是傾斜的，但切向分量保持連續。如果Bx=By=Bz=0，則成為普通流體力學的斜激波。如果激波強度趨於零,即ρ2/ρ1或p2/p1→1，則成為理想磁聲波。
同普通流體力學激波一樣，在磁流體力學激波中也存在聯繫激波前後兩側壓力和密度的關係式，稱為磁流體力學許貢紐關係式：
與普通流體力學激波相同，有關於ρ2/ρ1的條件：
左端的不等式ρ2/ρ1>1表示激波的壓縮性質(p2>p1>1)。
按激波速度來分，有三種可能的激波類型，即快激波、慢激波和中間激波。在快激波中，法向速度從超快磁聲速跳躍到亞快磁聲速，並且都是超阿爾文波速度的。在慢激波中，法向速度從超慢磁聲速跳躍到亞慢磁聲速，並且都是亞阿爾文波速度的。在中間激波中，激波前速度大於局部阿爾文波速度，而激波後速度小於局部阿爾文波速度。
通過激波之後，磁場的法向分量保持不變，而磁場的切向分量有不同的變化。因磁場切向分量不守恆，激波波陣面上一般有面電流。
以上關於激波的結論，都是以假定激波區域是無限薄為基礎的。其實，激波是有厚度的。由於激波是由壓縮波波陣面逐漸變陡而形成的，如果計及粘性和熱導等耗散效應，波陣面的變陡就會受到限制，結果達到一個平衡的永久波形，即形成一個具有一定厚度的激波過渡區。耗散係數愈小，激波愈接近於間斷面。在理論研究中，一般把激波結構分成三種情況：①如果電導率很高，則激波過渡區是一個寬度為幾個平均自由程的薄層，這就是前面討論過的情況；②如果電導率低且磁場大於某臨界值（依賴於激波強度），則激波過渡區較寬廣，所有物理量在越過激波時逐漸地變化；③如果電導率低且磁場小於該某臨界值，則產生一種可以明顯確定的陡峭的壓力激波，而磁場、速度、密度和溫度在越過此激波波前的一個寬的區域中緩慢地變化。
磁流體力學激波的實驗研究，一般採用電磁激波管。
參考書目
W.F.Hughes and F.J.Young,The Electromagnetodynamics of Fluids,John Wiley & Sons,New York,1966.
T.J.M.博伊德、J.J.桑德森著，戴世強、陸志雲譯：《電漿動力學》，科學出版社,北京，1977。(T.J.M. Boyd and J.J.Sanderson,Plasma Dynamics,Nelson,London,1969.)
H. Cabannes, Theoretical Magnetofluiddynamics,Academic Press,New York,1970.
