碎部點是測繪專業術語,用以描述地形的特徵。地形、地貌的平面輪廓由一些特徵點決定,這些特徵點統稱碎部點。
基本介紹
- 中文名:碎部點
- 外文名:detail point
- 解釋:測繪專業術語
- 性質:科學
- 類別:測繪
- 測量方法:極坐標法、方向交匯法等
簡介,測量方法,極坐標法,方向交匯法,距離交匯法,注意項目,
簡介
所謂碎部點就是地物、地貌的特徵點,如房角、道路交叉點、山頂、鞍部等。大比例尺地形圖測繪過程是先測定碎部點的平面位置與高程,然後根據碎部點對照實地情況,以相應的符號在圖上描繪地物、地貌。測量碎部點時,可以根據實際的地形情況、使用的儀器和工具選擇不同的測量方法。
碎部點應選地物、地貌的特徵點。對於地物,碎部點應選在地物輪廓線的方向變化處,如房角點,道路轉折點,交叉點,河岸線轉彎點以及獨立地物的中心點等。連線這些特徵點,便得到與實地相似的地物形狀。由於地物形狀極不規則,一般規定主要地物凸凹部分在圖上大於0.4mm均應表示出來,小於0.4mm時,可用直線連線。對於地貌來說,碎部點應選在最能反應地貌特徵的山脊線、山谷線等地性線上。如山頂、鞍部、山脊、山谷、山坡、山腳等坡度變化及方向變化處。根據這些特徵點的高程勾繪等高線,即可得地貌在圖上表示出來。
測量方法
碎部點的測量方法有極坐標法、方向交會法、距離交會法等。
極坐標法
極坐標法是根據測站點上的一個已知方向,測定已知方向與所求點方向的角度和量測測站點至所求點的距離,以確定所求點位置的一種方法。如右圖所示,設A、B為地面上的兩個已知點,欲測定碎部點(房角點)1、2、 、n的坐標,可以將儀器安置在A點,以AB方向作為零方向,觀測水平角
、n的坐標,可以將儀器安置在A點,以AB方向作為零方向,觀測水平角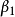 、
、 、
、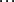 、
、 ,測定距離S1、S2、
,測定距離S1、S2、 、Sn,即可利用極坐標計算公式計算碎部點i ( i = 1、2、
、Sn,即可利用極坐標計算公式計算碎部點i ( i = 1、2、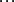 、n) 的坐標。測圖時,可按碎部點坐標直接展繪在測圖紙上,也可根據水平角和水平距離用圖解法將碎部點直接展繪在圖紙上。
、n) 的坐標。測圖時,可按碎部點坐標直接展繪在測圖紙上,也可根據水平角和水平距離用圖解法將碎部點直接展繪在圖紙上。
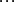
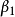
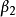


 極坐標法
極坐標法當待測點與碎部點之間的距離便於測量時,通常採用極坐標法。極坐標法是一種非常靈活的也是最主要的測繪碎部點的方法。例如採用經緯儀、平板儀測圖時常採用極坐標法。極坐標法測定碎部點時,適用於通視良好的開闊地區。碎部點的位置都是獨立測定的,因此不會產生誤差積累。
值得注意的是,由於全站儀的普及,它也可用於測定碎部點,這實際上也是極坐標法,不同的是它可以直接測定並顯示碎部點的坐標和高程,極大提高了碎部點的測量速度和精度,在大比例尺數字測圖中被廣泛採用。
方向交匯法
方向交會法又稱角度交會法,是分別在兩個已知測點上對同一碎部點進行方向交會以確定碎部點位置的一種方法。如圖(a)所示,A、B為已知點,為測定河流對岸的電桿1、2,在A點測定水平角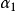 、
、 ,在B點測定水平角
,在B點測定水平角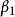 、
、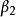 ,利用交會公式計算1、2點的坐標。也可以利用圖解法,根據觀測的水平角或方向線在圖上交會出1、2點,如圖(b)。方向交會常用於測繪目標明顯、距離較遠、易於瞄準的碎部點,如電桿、水塔、煙囪等地物。
,利用交會公式計算1、2點的坐標。也可以利用圖解法,根據觀測的水平角或方向線在圖上交會出1、2點,如圖(b)。方向交會常用於測繪目標明顯、距離較遠、易於瞄準的碎部點,如電桿、水塔、煙囪等地物。 方向交匯法
方向交匯法
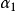

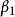
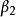
 方向交匯法
方向交匯法距離交匯法
距離交會法是測量兩已知點到碎部點的距離來確定來確定碎部點位置的一種方法。如圖(a)所示,A、B為已知點,P為測定碎部點,測量距離S1、S2後,利用距離交會公式計算P點坐標。也可以利用圖解法,利用圓規根據測量水平距離,在圖上交會碎部點,如圖(b)。 距離交匯法
距離交匯法
 距離交匯法
距離交匯法當碎部點到已知點(困難地區也可以為已測的碎部點)的距離不超過一尺段,地勢比較平坦且便於量距時,可採用距離交會的方法測繪碎部點。如城市大比例地形圖測繪、地籍測量時,常採用這種方法。
注意項目
對於碎部點的確定,就注意以下幾點:
1. 依比例的規則的建(構)築物只需測出三點,第四點可由計算機來完成。
2. 不規則的地貌應儘量能多測一些點,因為在傳統測圖中,一些細小的變化可通過手工來完成,但計算機的模擬是無法比較真實的反映出這些實際地形的。
3. 對於程式中規定順序繪製的圖塊,如橋樑,廣告牌等等,最好能按其順序進行測量。
此外,還應注意以下的一些事項:
1. 測圖單元的劃分,儘量以自然分界為界,如河流、道路等等,以便於地形圖的施測,也減少了接邊的問題。
2. 能夠測量到的點儘量實測,儘量避免用皮尺(鋼尺)量取。因為用全站儀所測量的速度遠非皮尺量取所能比的,而且精度也會高些。
3. 同一類地物(貌)應先測,以避免內業造成一些不必要的麻煩,當然,根據實地的實際情況,可作靈活的運用。同時,也方便測站上觀測人員的數字及字母輸入。
4. 測等高線時,除了測量特性線外,還應儘量多測一些加密的點,以滿足計算機建模的需要,也能更加詳盡地把映出地貌。
5. 由於數字測圖很多工作是在計算機上完成的,所以如何加強檢核是每個單位所就解決的。特別是在測區遠離內業地點時,必須有一定的措施。

