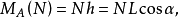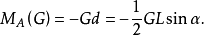矩心

物體的轉動中心叫做矩心。矩心到力的作用線的垂直距離叫做力臂。力與力臂的乘積叫做力矩。通常規定以使物體作逆時針轉動的力矩為正，以使物體作順時針轉動的力矩為負。在國際單位制中，力矩的單位是牛頓·米，用符號N·m表示。

基本介紹

• 中文名：矩心
• 外文名：centroid
• 特點：通過矩心的回歸線是最佳的回歸線
• 力矩為零：當力的作用線通過矩心時

力矩

力矩(moment of force)是力學的基本概念之一，是力使物體繞一點或一軸轉動的狀態發生改變的作用的度量，稱該點為矩心，該軸為矩軸。力對點的矩可表示為向量，它等於由矩心到力作用點所確定的向量和力向量的向量積，如圖1，

圖1

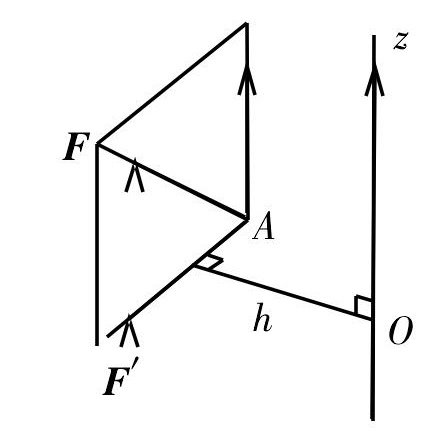圖2

力F作用點為A，矩心點為O，力對O的力矩為

其大小為 ，式中 是 到 的距離，稱為力臂。該力矩的方向是由 到 再到 ，符合右手螺旋法則。力對軸的矩是代數量，把力分解為平行和垂直於軸的兩個分量，垂直分量的大小乘以它與軸的距離即力矩大小，若垂直分量繞軸的轉向相對軸向符合右手螺旋法則，取正號，反之取負號；如圖2，力 相對z軸的垂直分量為 ，它到z的距離為h，力對z軸的矩為 ，若取 坐標系，令 為坐標軸上的單位向量，點A的坐標為 ，設 ，則

可見， 在z軸的投影為

正好等於 的垂直分量對z軸的力矩，亦即F對z軸的力矩 ，對其他軸亦有類似情形，故力對某軸上任一點的力矩在該軸的投影，就等於力對這個軸的力矩。力矩的單位在國際單位制中為 ，在工程單位制中為 。

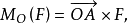
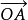
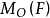
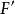
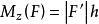
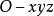
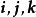
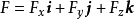
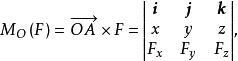
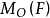
例題分析

【例1】圖示的桿AB，長度為L，自重不計，A端為固定鉸鏈支座，桿的中點C懸掛一重量為G的物體，B端支靠於光滑的牆上，其約束反力為N，桿與鉛直牆面的夾角為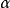 ，試分別求G和N對鉸鏈中心A點的力矩。

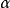
圖3

答：見圖3。

(1)畫出力N和G對矩心A的力臂h和d。

(2)計算力臂的大小

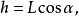
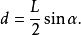
(3)計算力矩