眾和數,即一個自然數的各位數字之和。
基本介紹
- 中文名:眾和數
- 釋義:一個自然數的各位數字之和
- 規律:眾和數=九宮數=洛書數
- 例如:2013的眾和數是2+0+1+3=6
例如:
2013=2+0+1+3=6;
668的眾和數是6+6+8=20,2+0=2;
就是≥10的整數,求其眾和數。眾和數=九宮數=洛書數。
定義, 性質/定理以及發現的緣由,部分性質推廣:
1.設f(x)是這樣的一個映射,使得:表象數字的每一位進行求和。
即:令:x=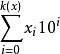 =
=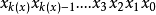 其中,
其中,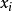 是表象數字
是表象數字
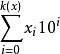
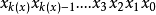
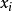
則有:f(x)=f(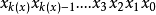 )=
)=
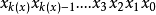

2.定義:n個f複合而成的函式為: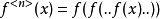 [ 其中,有n個f ]
[ 其中,有n個f ]
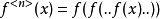
那么,必然存在一個最小的正整數 j ,使得: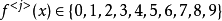
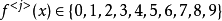
我們不妨令:g(x)=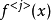
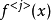
性質/定理:*1.周期性: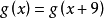 =......=
=......=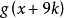 k為任意正整數
k為任意正整數
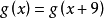
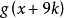
*2.餘數決定性: 若一個數 x除 9 所得餘數為:i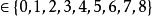
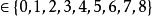
則: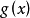 =
=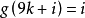
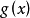
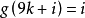
*3.間接映射性: 當 0<t<10 ,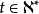
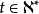
則: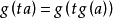 a為任意正整數
a為任意正整數
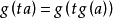
*4.類疊代性: 若x可以分解為n個數字的乘積: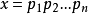 ,
,
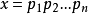
則: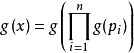
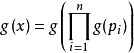
*5.可替換性:若存在下面形式的式子,其中是任意n個正整數字的乘積,則其中任意一項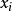 在
在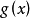 中可以被替換為
中可以被替換為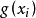
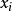
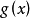
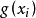
即: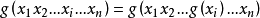 (注意,
(注意,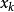 可以是
可以是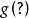 的形式)
的形式)
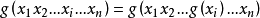
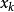
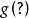
*6.若:0 < i< 10 , k 為任意正整數
則: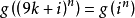 *
*
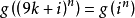
(註:3、4、5定理,均可以利用第1、2兩條來推出。讀者可以嘗試自行證明。)
發現緣由:筆者曾經看過一篇部落格,裡面講了一些關於數字與眾和數字的有趣性質。
它的第一行是: 1 2 4 8 16 32 64 128 256 512 1024 2048 .........
對應眾和數的後一行是:{1 2 4 8 7 5}{1 2 4 8 7 5}.........
因此,讀者與我都不難發現,經過眾和映射的後一行都是:{1,2,4,8,5,7}的周期循環。
而且,任意取一個數的後一行數,乘以2,取眾和映射,就恰好是後一個數的眾和數。
比如:512 對應 8 而8乘以2=16,取眾和映射,得到7 而7,恰好是2048對應的眾和數。
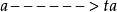

幸運的是,我在用餐時,想到了這樣一個有趣的發現:(這裡我隨意舉例)
71 x 89 = 6319
對應取f映射:(7+1)x(8+9).....(6+3+1+9) ;
即: 8 x 17....19
循環: 8 x8....10
即: 64....10
循環: 10....1
最終循環:1 = 1
不僅如此,筆者隨機驗證了3個數以上相乘對應的最終結果,都是:i=i的結果。
由此,我猜想這很可能是一個正確的定理。(事實上,這就是定理*4的雛形。)
然而,這些還不能證明兩個上述定理。因此,我開始初步分析函式: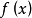 的性質。
的性質。
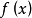
但,分析它的難度較大,因此,我決定先分析函式: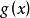 的特點規律:
的特點規律:
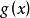
取這樣的二維數組: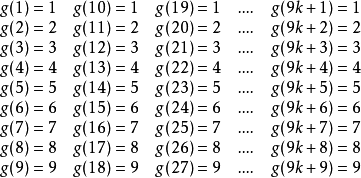
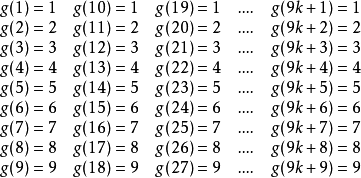
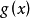
對定理1的證明比較枯燥,筆者不再多贅述。讀者可以自己證明。
筆者充分利用周期性,餘數特性,解決了第3,4定理的證明。(可以是歸納法)
由此,關於1,2,4,8,7,5的問題也就解決了。
部分性質推廣:實際上,不僅僅是: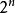 類型的眾和數有這樣的特點,任意數的n次方,其眾和數,都具有周期性。
類型的眾和數有這樣的特點,任意數的n次方,其眾和數,都具有周期性。
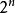
而且,僅在這些的循環方式中:
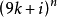
當:i = 2,對應:{1 2 4 8 7 5...}
當:i = 3,對應:{1 3 }{9...}
當:i = 4,對應:{1 4 7...}
當:i = 5,對應:{1 5 7 8 4 2...}
當:i = 6,對應:{1 6 }{9...}
當:i = 7,對應:{1 7 4...}
當:i = 8,對應:{1 8...}
當:i = 9,對應:{1 9...}
這些性質,留給讀者自行證明。我不再一一贅述。(提示:定理*6)
