研究稀薄氣體物理運動規律的理論。真空技術的理論基礎。主要採用統計物理和熱力學力一法研究稀薄氣體分子之間，分子與器壁之間的作用。內容包括漲落現象、分子速度和能量分布偏離常態理想氣體麥克斯韋分布的特點、真空技術中所涉及的嚴重的非平衡態、氣體與固體表而的相互作用等。
基本介紹
- 中文名：真空物理
- 外文名：Vacuum physics
理想氣體定律,氣體分子運動論基礎,蒸汽,氣體吸附,氣體流動,真空常用計算公式,
理想氣體定律
首先應該說明，本節及以後幾節中所介紹的定律和公式，是針對平衡狀態下的理想氣體得出的。不過，常溫(與室溫相比)低壓(相對大氣壓而言)下的各種氣體都可以看作是近似程度相當好地理想氣體，因此，我們可以放心地把這些定律和公式套用於真空工程的絕大部分計算之中。這其中包括通常所涉及到的各種氣體，甚至於接近飽和的蒸汽(如水蒸汽)；也包括各類氣體狀態過程，甚至於明顯的非平衡狀態(如氣體的流動過程)。
真空物理1、波義耳～馬略特定律：一定質量的氣體，若其溫度維持不變，氣體的壓力和體積的乘積為常數 pV = 常數。
2、蓋·呂薩克定律：一定質量的氣體，若其壓力維持不變，氣體的體積與其絕對溫度成正比 V/T = 常數 。
上述三個公式習慣上稱為氣體三定律。
具體套用方式常為針對由一個恆值過程連結的兩個氣體狀態，已知3個參數而求第4個參數。例如：初始壓力和體積為P1、V1，的氣體，經等溫膨脹後體積變為V2，則由波義耳--馬略特定律，可求得膨脹後的氣體壓力為P2 = P1V1/V2。這正是各種容積式真空泵最基本的抽氣原理。
4、道爾頓定律：相互不起化學作用的混合氣體的總壓力等於各種氣體分壓力之和。 P = P1 + P2+····+ Pn (4)這裡所說的混合氣體中某一組分氣體的分壓力，是指這種氣體單獨存在時所能產生的壓力。
道爾頓定律表明了個組分氣體壓力的相互獨立和可線性疊加的性質。
5．阿佛加德羅定律：等體積的任何種類氣體，在同溫度同壓力下均有相同的分子數；或者說，在溫度同壓力下，相同分子數目的不同種類氣體占據相同的體積。1mol任何氣體的分子數目叫做阿佛加德羅數，NA = 6.022×1023mol-1。在標準狀態下(po = 1.01325×105Pa，To = 0oC），1mol任何氣體的體積稱為標準摩爾體積，Vo = 2.24×10-2m3mol-1。
根據上述氣體定律，可得到反映氣體狀態參量p、V、T、m之間定量關係的理想氣體狀態方程： pV = m/M(RT) (5)式中的M為氣體的摩爾質量（kg/mol），R為普適氣體常數，R=8.31J/（mol·K）。在已知p、V、T、m四參量中的任意三個量時，可由此式求出另外一個值。例如氣體的質量m = pVM/（RT）
一定質量的氣體，由一個狀態（參量值為p1、V1、T1）經過任意一個熱力學過程(不必是恆值過程)變成另一狀態(參量值為p2、V2、T2)，根據狀態方程，可得到關係式：p1V1/T1 = p2V2/T2 (6)對（5）變換，還可計算單位體積空間內的氣體分子數目和氣體質量，即氣體分子數密度n（m-3）和氣體密度p（kg/m3） n = mNA/MV = pNA/RT = p/kT (7) p = m/V = pM/RT (8) 係數k = R/NA = 1.38×1023J/K 稱為波爾茲曼常數。
氣體分子運動論基礎
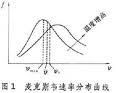
1. 處於平衡狀態的理想氣體分子，其熱運動速度的分布服從麥克斯韋速度分布定律。氣體分子熱運動率介於v～v+dv之間的幾率為dN/N = F（v）dv = 4π（mo/2πkT）3/2·exp·（-mov2/2kT）·v2dv (9)式中F（v）是速率v（m/s）的連續函式，稱為速率分布函式。mo = M/NA ，為一個氣體分子的質量(kg)。利用速率分布函式，可以計算出反映分子熱運動強度的三種特徵速率。最可幾速率vm 是在氣體分子所具有的各種不同熱運動速度中出現幾率最大的速度，即與F(v)最大值相對應的v值；所有氣體分子熱運動速度的算術平均值叫算術平均速度v；把所有氣體分子的速度的平方加起來，然後被分子總數除， 再開方就得到均方根速度vs。它們的計算公式如下： 2．理想氣體的壓力基本公式，將氣體分子微觀熱運動的強弱直接與巨觀上的氣體壓力定量聯繫起來：P = 1/3(nmovs2 = 1/3(pvs2) (11) 3．氣體中一個分子與其它分子每連續二次碰撞之間所走過的路程稱為自由程，自由程有長有短，差異很大，但大量自由程的統計平均值卻是一定的，稱為平均自由程頁λ(m)。單一種類氣體分子的平均自由程為(12-見下文) 如果是含有k種成份的混合氣體，則(13)式中σ是氣體分子的有效直徑(m)，下標l、j分別代表第1、j種氣體成份的參數。還可定義電子和離子在氣體中運動的平均自由程λe和λi(m)。需要強調說明的是，這裡所說電子或離子的自由程，是指電子或離子在氣體中運動時與氣體分子連續二次碰撞間所走過的路程，而沒有考慮電子或離子本身之間的碰撞，所以電子和離子平均自由程計算式中出現的都是氣體分子的參數，而與電子或離子的空間密度無關。(14)(15) 4．氣體分子的某一次自由程取值完全是隨機的，但大量自由程的長度分布卻服從一定的統計規律。氣體分子自由程大於一給定長度χ的幾率為(16)類似地可得出，電子或離子在氣體中運動的自由程大於一給定長度χ的幾率為(17)(18)利用這種分布規律，結合平均自由程計算公式(12)～(15)，可以計算出做定向運動的粒子束流穿過空間氣體時的散失率，或根據所限定的散失率確定空間氣體所必須達到的真空度。
真空物理
真空物理例如：一台離子束真空設備中，高能離子流由離子源射向25cm處的靶，若要求離子流與真空室內殘餘氣體分子碰撞的散失率小於5%，那么溫度為27oC的殘餘氣體壓力應為多少？
根據題意，可知當χ=O.25m時，要求 Pi(λi>χ)≥1%～5%，由(18)式，解出 exp(-0.25/λi)≥0.95，則 λi≥0.25/(-ln0.95)，即 λi≥4.87m。再將此結果代入(15)式得 kT/πσ2p≥4.87m；取空氣的分子有效直徑 σ=3.72 × 10-10m，則要求殘餘氣體壓力 p≤1.38 × 10-23 × 300/(π×3.722×10-20×4.87)，即p≤1.95 × 10-3Pa。
5．關於氣體分子對所接觸固體表面(如容器壁)的碰撞問題，可以從入射方向和入射數量二方面加以討論。若一立體角dw與面積元ds的法線間的夾角為θ，則單位時間內由dw方向飛來碰撞到ds上的氣體分子數目dNθ與cosθ成正比，這就是通常所說的餘弦定律：(19)單位時間內碰撞在固體表面單位面積上的氣體分子數目稱為氣體分子對表面的入射率ν(m-2s-1)，其計算式為：(20)根據平衡狀態的假設，氣體分子飛離固體表面時的方向分布及數量應與入射相一致，因此仍可按式(19)、(20)計算。克努曾餘弦反射定律還說明，不論氣體分子的入射方向怎樣
其反射都服從(19)式的餘弦規律。
6．如果兩個相連通的真空容器溫度不同，那么內部氣體達到狀態平衡時的參數也會有差異。在低真空條件下，即粘滯流態時，二容器的平衡條件是壓力相等，二容器內氣體壓力、溫度及分子數密度間關係為：p1 = p2 和 n1/n2 = T2/T1 (21)在高真空條件下，即分子流態時，二容器內氣體達到動力平衡的條件是在連通處的入射率γ相等，從而有關係：（22）
這種由於溫度不同而引起氣體流動，平衡時產生壓力梯度的現象，稱為熱流逸現象。它會給真空測量帶來誤差。例如某真空電阻爐熱場區溫度為1800K，通過細管連線的真空規管工作在300K溫度下，若規管測得壓強為2×10-4Pa，則可由(22)式算得爐內的真實氣體壓力為(22-1)
蒸汽
所謂蒸汽(又稱可凝性氣體)，是相對於永久氣體(或稱非可凝性氣體)而言的。對於任何一種氣體，都存在有一個臨界溫度，在臨界溫度以上的氣體，不能通過等溫壓縮發生液化，稱為永久氣體；而在臨界溫度以下的氣體，靠單純增加壓力即能使其液化，便是蒸汽。
空間中的蒸汽分子返回到液體內去的過程叫做凝結。蒸汽的凝結率W[kg/(m2
·s)]，即單位時間內在單位面積液面上凝結的蒸汽質量，可藉助(20)式計算(23)式中α為凝結係數，pv為蒸汽的分壓力。
蒸汽機
蒸汽機凝結的逆過程，即液體分子飛到空間變成蒸汽的現象，叫蒸發。單位時間通過單位面積液面蒸發的質量叫蒸發率Gv[kg/(m2·s)]在汽、液共存的條件下，蒸發和凝結現象同時存在，若蒸發率大於凝結率，則巨觀上表現為液體的蒸發；若蒸發率小於凝結率，則巨觀上
表現為蒸汽的凝結；二者相等時，則處於飽和狀態，此時空間蒸汽的壓力稱為對應平衡溫度下的飽和蒸汽壓ps。物質的飽和蒸汽壓隨著溫度的升高而增大。液體的蒸發率與對應溫度下的飽和蒸汽壓間的關係為 (24)此式常用於蒸發鍍膜中金屬蒸發量的計算。
一種蒸汽的實際壓力pv與其對應溫度下的飽和蒸汽壓ps之比，稱為蒸汽當時的飽和度。作為最常用的一項指標參數，常把空氣中水蒸汽的飽和度定義為空氣的相對溫度，相對溫度(%) = pvH20/psH20 × 100% (25)例如：工程中定義標準環境條件為溫度20oC，相對濕度65%，大氣壓力101325Pa。已知水蒸汽在20oC時的飽和蒸汽壓為2333Pa(17．5托)，則可計算出標準環境條件下大氣中水的分壓力為0.65 × 2333 = 1516Pa(11.375托)。
飽和蒸汽壓的存在，是蒸汽有別於理想氣體模型的根本之處，也是我們要將蒸汽的性質單獨作為一節討論的原因。在真空工程中，在蒸汽沒有達到飽和之前，即飽和度<1時，我們可以使用前面介紹的理想氣體定律和公式來描述蒸汽的性質；而蒸汽一旦達到飽和，情況卻大不相同，如果我們 對飽和蒸汽繼續作等溫壓縮，蒸汽壓力將不再升高而是維持飽和蒸汽壓的值不變，即不再服從波義耳--馬略特定律，為多餘部分的蒸汽將凝聚為液態或固態；反之，在飽和蒸汽與其凝聚相(液態或固態)平衡共存的情況下，對蒸汽作等溫膨脹，蒸汽的壓力也不會降低，而是其凝聚相不斷蒸發或升華來補充蒸汽，直至全部變成蒸汽為止。飽和蒸汽與其凝聚相間的這種等溫相變，尤其是水蒸汽的存在，在真空工程中有著不容忽視的影響。
蒸汽機
蒸汽機從上面的分析可知；在相聯通的真空系統中，如果某一處存在有揮發性較強的固體或液體，那么此處就相當於系統中的一個放氣源，使該物質在系統中的分壓力始終為對應溫度下的飽和蒸汽壓，這常常會限制系統極限真空度的提高；如果相聯通的真空系統各部分溫度不同，那么整個系統中蒸汽的分壓力都將與最低溫度所對應的飽和蒸汽壓相等，多餘的蒸汽物質最後都將凝聚在具有最低溫度的表面上，這正是低溫冷阱可以提高系統真空度的原理。
飽和蒸汽受壓縮時發生液化這一性質常給變容式真空泵的抽氣帶來困難，最突出的就是水蒸汽的抽除問題。以最常見的旋片泵為例：一個抽氣周期包括進氣腔膨脹吸氣、隔離和排氣腔壓縮排氣三步驟。如果吸入的氣體中水蒸汽的比例較大，在水蒸汽和永久氣體被壓縮達到排氣壓力之前，水蒸汽的分壓力已經達到飽和蒸汽壓，那么繼續壓縮的過程中，就會有一部分水蒸汽發生液化而混入泵油中，無法排出泵外，並且回到膨脹腔後還會在低壓下重新汽化成蒸汽，增大吸氣側的水蒸汽比例和壓力，導致泵的抽氣能力和極限真空的下降。若要保證水蒸汽能夠全部排出泵外而不發生液化，那么吸入的水蒸汽分壓力pv、永久氣體分壓力pp、對應泵溫下的水蒸汽飽和蒸汽壓A和泵的排氣壓力Pe間應滿足如下關係：pv / pv+pp<ps / pe 或 pv / pp < ps / pe-ps (26)例如：取泵的排氣壓強pe =1.1×lO5Pa，泵溫70oC時水的飽和蒸汽壓聲， ps=3.125×104Pa，則水蒸汽占吸入氣體的比例必須小於ps / pe=28.3%。在抽氣後期，尤其是空氣濕度較大時，這一條件很難達到。因為此時被抽容器內的永久氣體成份已經很少，但容器內表面凝結的水蒸汽卻不斷放出，所占比例就變得很大。解決這一問題的一個傳統方法是加氣鎮，即向壓縮腔內充入永久氣體成份以降低水蒸汽所占的比例，使其在達到飽和前便被排出。
蒸汽機
蒸汽機水蒸汽的存在也會影響到壓縮式真空計(麥氏計)的精確使用。測量讀數時，如果測量管內經過壓縮的氣體中，水蒸汽的分壓力尚低於當時飽和蒸汽壓，那么讀數表示的是水蒸汽和永久氣體的全壓力；若水蒸汽已經達到飽和發生液化，那么讀數會比永久氣體的分壓力高一些，但無法得到準確的數據。為消除水蒸汽對測量的干擾，常在麥氏計前安一低溫冷講，這樣測得的就只是永久氣體的分壓力。
液體(或固體)在真空中蒸發(或升華)變成蒸汽時需要吸收熱量，稱為汽化熱。物質的汽化熱隨著汽化溫度的升高而略有降低。比如lmol水，在50oC汽化，汽化熱為42780J，而在100oC汽化，汽化熱為40680J。蔬菜真空保鮮工藝中，讓蔬菜的一部分水份在真空中蒸發抽除，這些水蒸發時要從蔬菜體內吸取汽化熱，從而使蔬菜在脫水同時降溫，正是利用了水蒸發吸熱的原理；這種現象有時也會給真空操作帶來問題，比如在大型真空裝置中積存一些水，抽真空後一部分水蒸發成蒸汽排除，而這部分水吸收汽化熱使其餘的水降溫直至結冰，餘下的水就只能以升華的方式緩慢蒸發，從而延長抽真空的時間。
氣體吸附
氣體或蒸汽被固體表面浮獲而附著在表面上，形成單層或多層氣體分子層的現象叫做吸附。能捕集氣體的固體叫吸附劑，而被吸附的氣體成份叫吸附質。發生吸附作用的原因是由於在吸附劑表面存在著力場。根據吸附力的不同，氣體吸附可分為物理吸附和化學吸附。物理吸附是氣體分子受范德瓦爾斯力的吸引作用而附著在吸附劑表面之上，與氣體的液化過程相類似，其特點是吸附較弱，吸附熱較小，吸附不穩定，較易脫附，但對吸附的氣體一般無選擇性，溫度越低吸附量越大，能形成多層吸附，分子篩吸附泵和低溫泵的吸氣作用就屬於物理吸附。化學吸附是靠固體表面原子與氣體分子間形成吸附化學鍵實現的，與發生化學反應相類似，同物理吸附相比，化學吸附的特點是吸附強，吸附熱大，穩定不易脫附，吸附有選擇性，溫度較高時發生化學吸附的氣體分子增多，只能緊貼表面形成單層吸附(在化學吸附的分子上面還能形成物理吸附)，濺射離子泵和電子管中吸氣劑的吸氣作用就包括化學吸附。氣體吸附的逆過程，即被吸附的氣體或蒸汽從表面釋放出來重新回到空間的過程，稱為脫附或解吸。解吸現象可以是自然發生的，也可以是人為加速的。自然解吸有兩種情況，一是從巨觀平均地看，每個吸附氣體分子在表面停留一段時間後，都要發生脫附飛回空間，這時也會有其它氣體分子發生新的吸附，在氣體溫度、壓力一定的條件下，吸附速率與脫附速率相等，表面上的氣體吸附量維持恆定；另一種情況是在抽真空的過程中，空間氣體壓力不斷降低，表面上脫附速率大幹吸附速率，氣體吸附量逐漸減少，氣體從表面上緩緩放出，這種現象在真空中叫做材料的放氣或出氣。工程中最關心的問題是表面上的氣體吸附總量和抽空時的放氣速率，但至今還沒有很準確通用的計算方法，只能從實踐經驗中總結出：在低真空階段，表面吸附及表面放氣與空問氣體相比，數量很小，其影響可以忽略不計；在中真空階段，表面放氣量已接近空間氣體量，對二者應同樣重視；進入高真空乃至超高真空階段，表面放氣(不計系統漏氣時)已成為主要氣體負荷，放氣的快慢直接影響著抽空時間。通過人為的手段有意識地促進氣體解吸現象的發生，在真空技術中叫做去氣或除氣。人工去氣可以縮短系統達到極限真空的時間；可以獲得沒有氣體分子遮蓋的清潔表面。加熱烘烤去氣方法通過提高吸氣表面的溫度，增加分子熱運動能量來促進解吸，邊加熱邊排氣，常用於超高真空系統容器內表面及內部構件的去氣和真空電子器件內燈絲等內部金屬元件的去氣；離子轟擊去氣方法一般是在空間形成氣體放電，產生離子體區，使高能離子轟擊待清洗的固體表面，產生氣體濺射，使吸附氣體發生脫附，這是一種相當有效、簡捷迅速的除氣手段，在薄膜技術、表面科學等有氣體放電條件或有離子源的設備中廣泛採用。
氣體流動
當真空管道兩端存在有壓力差時，氣體就會自動地從高壓處向低壓處擴散，便形成了氣體流動。任何真空系統都是由氣源(待抽容器)、系統構件(管道閥門等)及抽氣裝置(真空泵)組成的，氣體從氣源經過系統的構件向抽氣口源源不斷地流動，是動態真空系統的普遍特點。
真空技術中，氣體沿管道的流動狀態可劃分為如下幾種基本形式：從大氣壓力下開始抽真空的初期，管道中氣體壓力和流速較高，氣體的慣性力在流動中起主要作用，流動呈不穩定狀態，流線無規則，並不時有旋渦出現，這種流動狀態稱為湍流(渦流，紊流)；隨著流速和氣壓的降低，在低真空區域內，氣流由湍流變成規則的層流流動，各部分具有不同速度的流動層，流線平行於管軸，氣體的粘滯力在流動中起主導作用，此時氣體分子的平均自由程λ仍遠小於導管最小截面尺寸d，這種流態叫做粘滯流；當氣體流動進入高真空範圍，分子平均自由程λ遠遠大於管道最小尺寸d時，氣體分子與管壁之間的碰撞占居主要地位，分子靠熱運動自由地直線進行，只發生與管壁的碰撞和熱反射而飛過管道，氣體流動由各個分子的獨立運動疊加而成，這種流動稱作分子流；發生在中真空區域內，介於粘滯與分子流之間的流動狀態叫做中間流或過渡流。
在不同的流動狀態下，管道中的氣體流量和導氣能力計算方法不同，因此在氣體流動計算時，首先要進行流態判別。由於在真空抽氣過程中湍流的出現時間較短，常常不加以單獨考慮，而是將其歸入粘滯流態。其它流動狀態的判別可用克努曾數λ/d 或管道中平均壓力p與幾何尺寸d的乘積pd作為判據：
粘滯流 λ/d100 pd>1Pa·m中間流 1/100<λ/d<1/3 0.03Pa·m<pd<1Pa·m (27)分子流 λ/d<1/3 pd<0.03Pa·m
為了考察管道中流過的氣體數量的多少，可以使用氣體的質量流率qm(kg/s)和摩爾流率qv(mol/s)，即單位時間內通過管道某一截面的氣體質量和氣體摩爾數。不過這兩種流率不便實際測量，因此工程中廣泛使用的是單位時間內流過管道指定截面的氣體體積，即體積流率qv(m3/s)。在氣體壓力為p的截面上，qv與qm、qγ的關係為 qm = pM/RT·qv 和 qv = p/RT·qv (28)在真空泵入口處的氣體體積流率又稱為泵的抽氣速率(簡稱抽速)，是真空泵的重要性能指標之一。由於在不同壓力下，相同的體積流率對應有不同的質量流率，所以在計算體積流率量值時，必須指明所對應的氣體壓力。
為了更方便地計算流過氣體的多少，工程中還定義氣體的壓力與其體積的乘積為氣體量G(Pa·m3=J)，即G=pV；單位時間內流過指定橫截面的氣體量為流量qG=dG/dt(Pa·m3/s=J/s)；在任一指定截面上，氣體流量、壓力和抽速間的關係為 qG = p·qv (29)在穩定流動狀態下，即管道各截面處的氣體壓力不隨時間變化時，根據質量守恆原理，真空系統任一截面上的氣體質量流率qm相等，若整個系統中各處溫度相同，則化為流量連續方程，即各截面上的氣體流量相等。 qG = p1qv1 =p2qv2 =piqvi (30)如果氣體流動過程中溫度有變化，例如流過冷卻器後溫度由T1降至T2，則對應的流量qG1/T1=qG2/T2實驗說明，氣體流過一段真空管道的流量qG與管道兩端的壓力差p1-p2成正比，即有 qG=C·(p1-p2) (31) 式中的比例係數C具有體積流率的量綱（m3/s)，它所反映的是管道允許流過氣體能力的大小，定義為該段管道的流導。流導是各種真空系統元件（管道、閥們、冷阱、孔口等）的主要技術指標之一，直接反映該元件對氣體流動的阻礙程度，是真空系統計算中需要首先計算的參數。元件的流導與所流過氣體的流動狀態有關，氣體流動為粘滯流時，流導值與元件的幾何結構尺寸及流過氣體的平均壓力有關；為分子流時，流導僅與幾何結構尺寸有關。根據組成真空系統的需要，有時將幾個真空元件(如管道)的入口和出口分別聯接在一起，稱為元件的並聯，並聯後元件的總流導等於各分支流導之和 C=C1+C2+…+Cn (32)有時將幾個元件首尾順序聯接，稱為元件的串聯，串聯後元件的總流導的倒數等於各元件流導的倒數之和 1/C = 1/C1+1/C2+…+1/Cn (33)把一個被抽容器的出口和一台真空泵的入口，用總流導為C的真空管路聯接起來，若真空泵在其入口處的抽速為S，則該真空系統在被抽容器出口處所能產生的有效抽速為S，則該真空系統在被抽容器出口處所能產生的有效抽速Se為 Se = (S·C)/(S+C) (34)此式習慣上稱為真空技術基本方程。從中可以看出，在被抽容器出口產生的有效抽速Se，比泵口抽速S和管路流導C都要小；若要獲得較大的Se，應該合理地搭配S和C，單獨增大其中的一個，不能獲得理想的結果
真空常用計算公式
1、玻義爾定律
體積V，壓強P，P·V=常數
一定質量的氣體，當溫度不變時，氣體的壓強與氣體的體積成反比。
即P1/P2=V2/V1
2、蓋·呂薩克定律
當壓強P不變時，一定質量的氣體，其體積V與絕對溫度T成正比：
V1/V2=T1/T2=常數
當壓強不變時，一定質量的氣體，溫度每升高(或P降低)1℃，則它的體積比原來增加(或縮小)1/273。
3、查理定律
當氣體的體積V保持不變，一定質量的氣體，壓強P與其絕對溫度T成正比，即：
P1/P2=T1/T2
在一定的體積下，一定質量的氣體，溫度每升高(或降低)1℃，它的壓強比原來增加(或減少)1/273。
4、平均自由程：
λ=(5×10-3)/P (cm)
5、抽速：
S=dv/dt (升/秒)或 S=Q/P
Q=流量(托·升/秒) P=壓強(托) V=體積(升) t=時間(秒)
6、通導：
C=Q/(P2-P1) (升/秒)
7、真空抽氣時間：
對於從大氣壓到1托抽氣時間計算式：
t=8V/S (經驗公式)
V為體積，S為抽氣速率，通常t在5~10分鐘內選擇。
8、維持泵選擇：
S維=S前/10
9、擴散泵抽速估算：
S=3D2 (D=直徑cm）
10、羅茨泵的前級抽速：
S=(0.1~0.2)S羅 (l/s)
11、漏率：
Q漏=V(P2-P1)/(t2-t1)
Q漏－系統漏率(mmHg·l/s)
V－系統容積(l)
P1－真空泵停止時系統中壓強(mmHg)
P2－真空室經過時間t後達到的壓強(mmHg)
t－壓強從P1升到P2經過的時間(s)
12、粗抽泵的抽速選擇：
S=Q1/P預 (l/s)
S=2.3V·lg(Pa/P預)/t
S－機械泵有效抽速
Q1－真空系統漏氣率(托·升/秒)
P預－需要達到的預真空度(托)
V－真空系統容積(升)
t－達到P預時所需要的時間
Pa－大氣壓值(托）
13、前級泵抽速選擇：
排氣口壓力低於一個大氣壓的傳輸泵如擴散泵、油增壓泵、羅茨泵、渦輪分子泵等，它們工作時需要前級泵來維持其前級壓力低於臨界值，選用的前級泵必須能將主泵的最大氣體量排走，根據管路中，各截面流量恆等的原則有：
PnSg≥PgS 或
Sg≥Pgs/Pn
Sg－前級泵的有效抽速(l/s)
Pn－主泵臨界前級壓強(最大排氣壓強)(l/s)
Pg－真空室最高工作壓強(托)
S－主泵工作時在Pg時的有效抽速。(l/s)
14、擴散泵抽速計算公式：
S=Q/P=(K·n)/(P·t)(升/秒)
式中：S－被試泵的抽氣速率(l/s)
n－滴管內油柱上升格數(格)
t－油柱上升n格所需要的時間(秒)
P－在泵口附近測得的壓強(托)
K－滴管係數(托·升/秒)
K=V0·(L/n)·(Υ0/Υm)+Pa△Vt
其中V0－滴管和真空膠管的原始容積(升)
L－滴管刻度部分的長度(mm)
n－滴管刻度部分的格數(格)
Υ0－油的比重(克/厘米3)
Υm－汞的比重(克/厘米3)
Pa－當地大氣壓強(托)
△Vt－滴管的刻度上的一格的對應的容積(升/格)
15、旋片真空泵的幾何抽速計算公式：
S=πZnLKv(D2-d2)/(24×104) (l/s)
式中：Z為旋片數，n為轉速(轉/分)，L為泵腔長度，D為泵腔直徑，d為轉子直徑(cm)，Kv為容積利用係數(一般取95%)。
16、O型橡膠槽深B=0.7D
D為橡膠直徑，槽寬C=1.6B
17、方形橡膠槽深B=0.8A
A為方形橡膠邊長，槽寬C=1.67B
