基本介紹
- 中文名:直角射影定理
- 外文名:projection theorem of a rightangle to a plane
- 所屬學科:數學
- 所屬問題:立體幾何
基本介紹,相關分析,
基本介紹
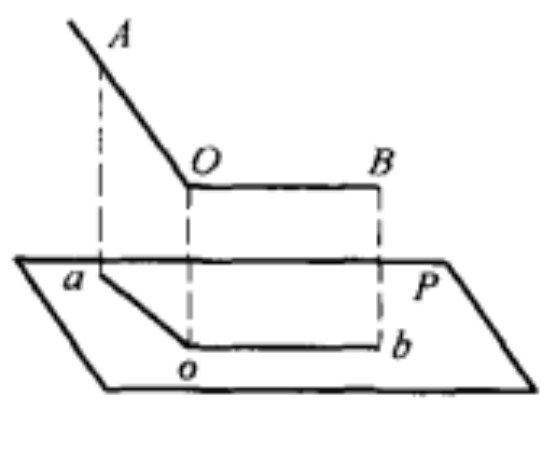
直角射影定理:一個直角在一個平面上的射影仍是直角的充要條件是:它至少有一邊平行於射影平面。如圖1所示,∠ABC=90°(即AB⊥BC),M為射影平面,∠ABC在平面M上的射影為∠A'B'C',直角射影定理告訴我們:如果BC//平面M或AB//平面M,則∠A'B'C'=90°;反之,如果∠A'B'C'=90°,則可斷定邊AB、BC中至少有一邊與平面M平行。
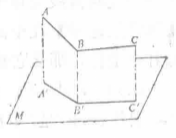
圖1
相關分析
直角射影定理:一個直角投影為直角的充要條件是:它至少有一邊平行於射影平面。
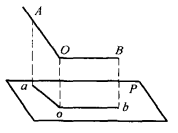
圖2
(1)設∠AOB(圖2)為直角,它的邊OB平行一平面P,而它在這平面上的射影是∠aob。平行於OB的直線ob和兩條相交線OA,Oo垂直,因此它垂直於平面OAao,因而也垂直於oa。
(2)設直角∠AOB投射在平面P上成直角∠aob,因直線ab垂直於oa和Oo,故它垂直於平面OAao,因而垂直於OA,由於OA也垂直於OB,若設OB和ob不相平行,OA就垂直於平面OBbo、因而(根據下面的定理的推論1)平行於平面P。在相反的情況下,與平面P平行的是OB。
定理1若兩平面垂直,則在一平面上所引它們交線的垂線必垂直於另一平面。
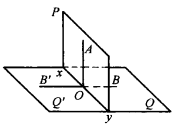
圖3
設PxyQ(圖3)為一直二面角,並設OA是在平面P上所引垂直於xy的直線,這直線OA可視為二面角PQ的平面角的一邊,因之垂直於這角的第二邊,它既已垂直於xy,就垂直於平面Q了,證畢。
上面定理的假設可看做由兩部分構成,即(1)兩平面P和Q互相垂直;(2)交線的垂線OA位於平面P上。
因此這定理有兩個逆定理。
第一逆定理一平面若含第二平面的一條垂線,則垂直於第二平面。
若平面P含平面Q的垂線OA,它就與平面Q垂直,因為二面角PQ的平面角∠AOB是直角。
第二逆定理 若兩平面垂直,則由一平面上一點引另一平面的垂線,必整個含在第一平面上。
設平面P和Q垂直,從平面P上一點A所引平面Q的垂線,其實就是由點A所引兩平面交線的垂線。
推論1 推廣言之,若一平面平行於另一平面的一條垂線,則必垂直於此平面。
若平面P平行於平面Q的一條垂線D,則必含D的一條平行線,於是垂直於Q(第一逆定理)。
垂直於同一平面的直線和平面彼此平行,因為其中一個含(第二逆定理)另一個的一條平行線。
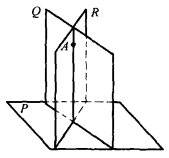
圖4
推論2 若兩相交平面垂直於第三平面,則其交線垂直於這第三平面。
設兩平面Q和R(圖4)都垂直於P,而A為其公共點之一,則由點A所引P的垂線含於Q及R上(第二逆定理),因此這垂線就是它們的交線。