無窮乘積機率空間:數學術語
基本介紹
- 中文名:無窮乘積機率空間
- 外文名:infinite product probabili-ty space
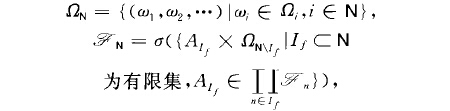
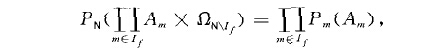
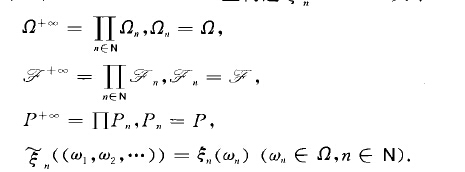
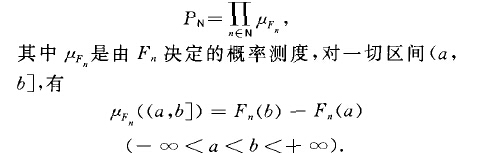
無窮乘積機率空間:數學術語
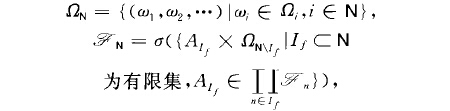
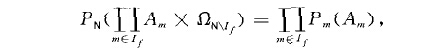
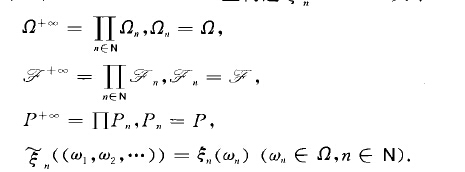
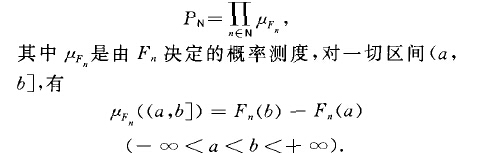
無窮乘積機率空間:數學術語無窮乘積機率空間 (infinite product probabili-ty space)機率論特有的由無窮多個機率空間構造無窮維機率空間的方法.設(,fl..,.} ,P,.) (nEN)是...
3.4 r次平均與Lr空間 3.4.1 幾個重要不等式 3.4.2 Lr空間 3.4.3 與各種收斂性之間的關係 3.5 可加集函式的分解 53.5.1 可加集函式的分解定理 3.5.2 不定積分與Lebesgue分解定理 3.5.3 分布函式的分解定理 3.6 補充與習題 第四章 乘積測度空間 4.1 Fubini定理 4.2 無窮乘積機率空間 4.3...
3.6 γ次平均收斂與空間Lγ 3.7 不定積分與σ-可加集函式的分解 第4章 乘積測度空間 4.1 有限維乘積測度 4.2 Fubini定理 4.3 無窮乘積機率空間 第5章 條件機率與條件數學期望 5.1 初等情形 5.2 給定σ-代數下條件期望與條件機率的定義和性質 5.3 給定函式下的條件數學期望 5.4 轉移機率與...
第六章 乘積測度與無窮乘積機率空間 6.1 乘積測度與轉移測度 習題 6.1 6.2 Fubini定理及其套用 習題 6.2 6.3 無窮維乘積機率 習題 6.3 第七章 不定積分與條件期望 7.1 符號測度的分解 習題 7.1 7.2 Lebesgue分解定理與Radon-Nikodym定理 習題 7.2 7.3 條件期望的概念 習題 7.3 7.4 條件期望的...
機率論基礎;第三部分,機率極限理論 . 第一部分包括前四章:測度空間與機率空間;可測映射與隨機變數;積分與期望;乘積空間與 Fubini定理. 第二部分包括兩章:獨立性、條件期望、一致可積性;鞅論簡介 . 第三部分包括兩章:大數定律;中心極限定理. 另外,將用一章介紹 Chebyshev不等式,最後一章介紹機率論...
《測度論講義》是2004年8月1日科學出版社出版的圖書,作者是嚴加安。 內容簡介 《測度論講義(第二版)》系統介紹一般可測空間和Hausdorff空間上的測度與積分、測度的弱收斂和淡收斂,以及與測度論有關的機率論基礎知識。第二版增加了第8章和第9章,分別介紹離散時間鞅、Hilbert空間和Banach空間上的測度。《測度論...
