準動量守恆

在晶體x射線衍射過程中，有兩種不同的模型，分別衍生出勞埃定理和布拉格定理。其中勞埃定理將每一個被x射線照射的格點作為次級發射源，次級光互相干涉，所以得到的衍射面為一系列同軸圓錐。布拉格定理認為入射光在一系列晶面上發生反射，同族晶面的反射光互相干涉。由布拉格定理和倒格矢的定義可以得到在衍射過程中的動量關係。

基本介紹

• 中文名：準動量守恆
• 外文名：quasi momentum conservation
• 表達式：p'-p=±hq±hGn
• 套用學科：物理學
• 適用領域範圍：晶體學
• 適用領域範圍：固體物理

布拉格定律

布拉格定律是晶體衍射的基本定律，如左圖所示。發生干涉的條件是光程差為波長的整數倍。令BCD= ，

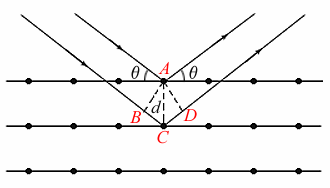布拉格定律示意圖

所以由幾何關係可得：

這就是布拉格定律。

公示

為了晶體學，尤其是晶體衍射的研究的方便，物理學上引入了在倒空間，或者說是動量空間的矢量，稱為倒格矢。

現在考慮一個密勒指數為(h k l)的面，三個基矢分別是a,b,c。根據密勒指數的定義，則這個晶面在三個坐標軸上的截距分別是a/h,b/k,c/l。設晶面的兩條邊分別是 和 ,其中下劃線表示矢量，則這個晶面的法線就是這兩個矢量的外積， x 。

由於我們只是想要求得法線，所以括弧前的係數可以不失一般性地略去。

注意到兩個基矢的叉乘實際上是晶胞的一個底面。可以同時除以晶胞體積進行歸一化，得到的是晶面間距的倒數。

由此得到晶面法線矢量：

等號右邊即為倒格矢。由表達式可以看出，本質上倒格矢是將實空間中的晶面轉換為倒空間中的格點。

如果用倒格矢基矢的形式表達，即為：

至此，倒空間與實空間有了一致的形式。

關係推理

為了後續討論的方便，不妨把倒格矢基矢和倒格矢同乘 。s.t.

參考概述中的示意圖，現在考慮x射線的波矢 。

根據幾何關係可以推得：

在化簡過程中使用了布拉格定律以及倒格矢和面間距的關係： （可由幾何關係得到）

由此可以看出，x射線衍射過程中波矢的改變即為倒格矢。再利用由德布羅意關係推出的（其中h為約化普朗克常量），就可以得到衍射過程中的動量守恆表達式：

討論

如果考慮聲子的動量，得到更一般的表達式，即準動量守恆表達式：

稱為聲子的準動量。

一般說來，聲子的準動量並不代表真實的動量，只是它的作用類似於動量，如上式所示，在中子吸收和發射聲子過程中，存在類似於動量守恆的變換規律，但是，多出±hGn項。動量守恆是空間均勻性（或者稱為完全的平移不變性）的結果，而上述準動量守恆關係實際上是晶格周期性（或者稱為晶格平移不變性）的反映。一方面，由於晶格也具有一定的平移對稱性（以布拉伐格子標誌），因而存在與動量守恆相類似的變換規律；另一方面，由於晶體平移對稱性與完全的平移對稱性相比，對稱性降低了，因而變換規則與動量守恆相比，條件變弱了，可以相差±hGn。