物理學中，湯姆孫散射是指電磁輻射和一個自由帶電粒子產生的彈性散射。入射電磁波的電場使粒子加速，從而激發粒子產生和入射波頻率相同的輻射（散射波）。湯姆孫散射是康普頓散射在低能量區的近似。湯姆孫散射是等離子物理學中的一個重要現象，它首先由英國物理學家約瑟夫·湯姆孫解釋。只要粒子的運動是非相對論性的（即速度遠小於光速），粒子加速的主要原因都來自入射波的電場分量，而磁場的作用可被忽略。粒子將會在電場振動的方向上開始運動，從而產生電磁偶極輻射。運動粒子在垂直於運動方向上的輻射最強，而輻射沿著粒子的運動方向產生偏振。從而，取決於觀察者的位置，從一個小體元散射出的電磁波存在程度不同的偏振。
基本介紹
- 中文名：湯姆孫散射
- 外文名：Thomson scattering
- 學科：物理學
- 定義：康普頓散射在低能量區的近似
- 提出者：約瑟夫·湯姆孫
- 有關術語：電磁輻射
簡介,湯姆孫散射的實例,康普頓散射,
簡介
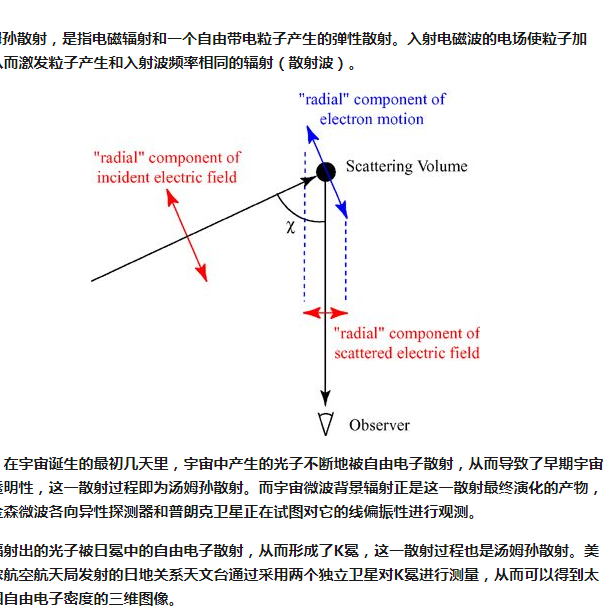
在湯姆孫散射中，入射波和觀察到的散射波電場都可以分解為位於觀察平面（由入射波傳播方向和散射波傳播方向構成的平面）內和垂直於觀察平面的分量。習慣上，那些位於平面內的分量被稱作“徑向”，而垂直於平面的分量被稱作“切向”，這都是對於觀察者而言的。
圖1所示的是散射在觀察平面內的情形，圖中顯示了入射電場的徑向分量是造成位於散射點的帶電粒子在該方向上發生運動的原因，並且這一運動也位於觀察平面內。此外還可以看出散射波的振幅正比於入射波與散射波夾角χ的餘弦，而散射波的光強正比于振幅的平方，從而含有cos2(χ)這一因子。而垂直於觀察平面的切向分量則不會產生類似的影響。
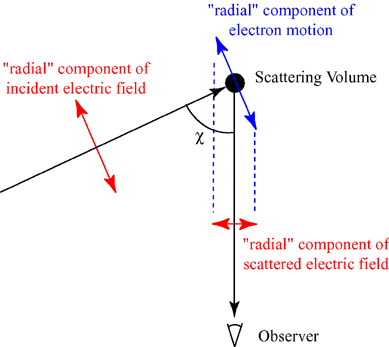
圖1
描述散射的最佳方法是引入一個發射係數
，而是在時間間隔dt內被體元
散射至立體角 
這一方向內，且波長介於
和 
之間的入射波能量。從觀察者的角度而言，湯姆孫散射存在有兩個發射係數，一個是對應著徑向偏振波的發射係數 
,，另一個是對應著切向偏振波的發射係數
。它們分別由下面關係給出：
其中n是位於散射點的帶電粒子密度，I是入射波的通量（單位時間單位波長範圍內輻射到單位面積的能量）。而σ是帶電粒子的湯姆孫散射的微分截面（面積/立體角），其表達式為
注意到這正是一個具有質量m和電荷q的點粒子的經典半徑。對於電子而言，散射微分截面為
這裡 {\displaystyle \lambda _{e}}是電子的康普頓波長。
散射波輻射出的總能量可通過對發射係數求和並對空間中所有方向積分給出：
這裡σT是總散射截面。
對於電子而言，這個散射截面為
湯姆孫散射的實例
在宇宙誕生的最初幾天裡，宇宙中產生的光子不斷地被自由電子散射，從而導致了早期宇宙的不透明性，這一散射過程即為湯姆孫散射。而宇宙微波背景輻射正是這一散射最終演化的產物，威爾金森微波各向異性探測器和普朗克衛星正在試圖對它的線偏振性進行觀測。
康普頓散射
在原子物理學中，康普頓散射，或稱康普頓效應（英語：Compton effect），是指當X射線或伽馬射線的光子跟物質相互作用，因失去能量而導致波長變長的現象。相應的還存在逆康普頓效應——光子獲得能量引起波長變短。這一波長變化的幅度被稱為康普頓偏移。康普頓效應通常指物質電子云與光子的相互作用，但還有物質原子核與光子的相互作用——核康普頓效應存在。康普頓效應首先在1923年由美國華盛頓大學物理學家康普頓觀察到，並在隨後的幾年間由他的研究生吳有訓進一步證實。康普頓因發現此效應而獲得1927年的諾貝爾物理學獎。
這個效應反映出光不僅僅具有波動性。此前湯姆孫散射的經典波動理論並不能解釋此處波長偏移的成因，必須引入光的粒子性。這一實驗說服了當時很多物理學家相信，光在某種情況下表現出粒子性，光束類似一串粒子流，而該粒子流的能量與光頻率成正比。
在引入光子概念之後，康普頓散射可以得到如下解釋：電子與光子發生彈性碰撞（彈性碰撞產生的非彈性散射），電子獲得光子的一部分能量而反彈，失去部分能量的光子則從另一方向飛出，整個過程中總動量守恆，如果光子的剩餘能量足夠多的話，還會發生第二次甚至第三次彈性碰撞。
康普頓散射可以在任何物質中發生。當光子從光子源發出，射入散射物質（一般指金屬）時，主要是與電子發生作用。如果光子的能量相當低（與電子束縛能同數量級），則主要產生光電效應，原子吸收光子而產生電離。如果光子的能量相當大（遠超過電子的束縛能）時，則我們可以認為光子對自由電子發生散射，而產生康普頓效應。如果光子能量極其大（>1.022百萬電子伏特）則足以轟擊原子核而生成一對粒子：電子和正電子，這個現象被稱為成對產生。
由於光子具有波粒二象性，因此，應該可以用波動理論詮釋這效應。埃爾溫·薛丁格於1927年給出半經典理論。這理論是用經典電動力學來描述光子，用量子力學來描述電子。
