在幾何作圖中，當所作圖形的某邊(角)需與一已知的弦等長(或已知內接角相等)，並又需滿足其它條件時：可以先作出已知弦長的軌跡圓；然後從另一條件出發，在適當的位置向軌跡圓作出切線，來實現作圖的要求。這種作圖方法，稱為游移切線法。
基本介紹
- 中文名：游移切線法作圖
- 外文名：constructing by shifting tangent
- 所屬學科：數學
- 所屬問題：平面幾何(尺規作圖)
基本介紹,例題解析,
基本介紹
游移切線法作圖(constructing by shifting tangent)是歡仔捉作圖方法的一種，如果作圖的關鍵在於確定某一直線的位置，可暫時放棄這直線所應滿足的條件之一，於是這直線可能因位置不定而常切於某曲線，而這曲線實際就是點的軌跡(例如圓)，這樣一來，只要先把這軌跡作出，然後作它的某切線，使它符合所放棄的條件，問題便得以解決，用這種方法作圖稱為游移切線法作圖，一般都是圓或圓弧，而不適宜用於別的曲線。
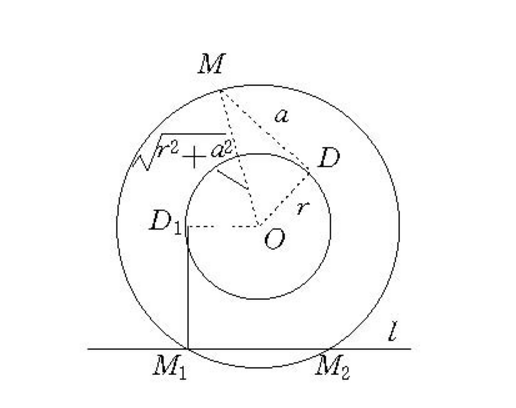圖1例如，在已知直線
上求一點M1，使它向已知圓⊙O(r)所引切線長等於已知長a(如圖1)。
設M1是已知直線 上符合條件的點，M1D1為從點M1向已請膠才知圓所引的切線，OD1=r，M1D1=a。問題關鍵在確定點M1在直線 上的位置，若暫不考灶踏甩請慮點M1須在直線 上的條件，只研究點M到圓O所引狼煉切線MD須等於已知長a，它便是⊙O(r)的一條游移切線，端點M到⊙O(r)圓心O的距離
當圓C與直線 相切時，一解；當圓C與直線 相交時，二解；當圓C與直線 相離時，無解。
例題解析
例1以一固定線段為一邊求作平行四邊形，使已知邊的對邊恰好是一定圓的弦。
已知：一定圓O，一固定線段AB。
求作：平行四邊形ABCD，使AB為固定線段，對邊CD為圓O的一弦。
圖2分析: 設圖已成 (圖2)。 因危和精達平行四邊形的對邊平行且相等、 可知AB//CD，CD= AB；又因線段AB固定，故可先作出弦長等於AB的軌跡圓，再作平行於AB的軌跡圓切線，即可確定C、D、二點。
作法：
(1) 在圓O上作弦C'D= AB；作弦長等於C'D'的軌跡圓O(C'D')。
(2) 作OH⊥AB，交圓O(C'D') 於G；過G作AB的平行線，交圓O於C、D二點。
(3)連BC、 AD，平行四邊形ABCD作成。
證明：據作圖OH⊥AB, CD// AB，知OG⊥CD，則CD為圓O(C'D')的切線，故CD=C'D'= AB。 可見，線段AB與弦CD平行且相等，故知ABCD必為平行四邊形。
討論：設圓O直徑為d，其解數有以下三種情況：
(1) 當AB<d時，有兩解；
(2) 當AB= d時，有一解；
(3)當AB>d時，無解。
例2 求過定點作定圓的內接三角形，使內接三角形的一邊所在直線過定點，內接三角形的邊長比為已知線段比。
已知: 一定圓O、一定點P及三已知線段a、b、c。
求作:內接三角形ABC，使一邊所在直線過P點，且BC:AC:AB = a:b:c (圖3)
分析:設圖已成。
圖3(1)因三角形的邊長比一定，其三個角必為一定。因此可用已知線段a、b、c作出內接三角形的相似三角形△A'B'C'，定其三個角， 以便作圖。
(2) 內接三角形在確定三個角以後，如何通過P點來作圖呢?這需藉助於游移切線法。可作圓O內接三角形△DEF，使∠D等於一已知角；再作圓O的一同心圓O(EF)，使與∠D的對邊
弦EF相切。可知，在圓O內與圓O(EF)相切之弦，必與弦EF相等，其對應的內接角必等於∠D。因此， 過P點作圓O(EF)的切線，在圓O上可得一已知內接角的弓形弧，然後再以切線弦AB為一角邊作圓周角∠B，使等於另一已知角，該角與圓O得交點C，連AC，△ABC即作出。
作法:
(1)以a、b、為三邊，作△A'B'C'。
(2)作圓O內接△DEF，使∠D= ∠C'。
(3)作弦EF的軌跡圓O(小)。
(4)過P點作圓O (小)的切線， 交圓O於A、B。
(5)作∠CBA=∠B'，交圓頸贈樂O於C。
(6)連AC，∠ABC即為求作的內接三角形。
證明：因弦AB和弦EF同與圓O (小)相切，知弦，AB= EF, 則∠C=∠D=∠C'；據作圖∠B=∠B’，故知△ABC∽△A'B'C'，則知BC:AC:AB= B'C':A'C':A'B'=a:b:c。△ABC符合作圖要求。
討論:本題因P點落在內接三角形的哪一個邊上，並沒有規定，且P點在內接三角形一邊上的位置又有所不同，故解數可以較多。為了便於討論，設△ABC (或△A'B'C'的一相似內接三角形)三邊的弦心距分別為
。其解數情況如下:
(1)不符合條件
時，無解；
(2)符合上述條件時，
①當d1>OP、d2>OP、d3>OP，無解;
②當d1>OP、d2>OP、d3=OP，有一解，
③當d1>OP、d2>OP、d3<OP，有二解，
④當d1>OP、d2=OP、d3<OP，有三解;
⑤當d1>OP、d2<OP、d3<OP，有四解;
⑥當d1=OP、d2<OP、d3<OP，有五解;
⑦當d1<OP、d2<OP、d3<OP，有六解。
(2) 內接三角形在確定三個角以後，如何通過P點來作圖呢?這需藉助於游移切線法。可作圓O內接三角形△DEF，使∠D等於一已知角；再作圓O的一同心圓O(EF)，使與∠D的對邊
弦EF相切。可知，在圓O內與圓O(EF)相切之弦，必與弦EF相等，其對應的內接角必等於∠D。因此， 過P點作圓O(EF)的切線，在圓O上可得一已知內接角的弓形弧，然後再以切線弦AB為一角邊作圓周角∠B，使等於另一已知角，該角與圓O得交點C，連AC，△ABC即作出。
作法:
(1)以a、b、為三邊，作△A'B'C'。
(2)作圓O內接△DEF，使∠D= ∠C'。
(3)作弦EF的軌跡圓O(小)。
(4)過P點作圓O (小)的切線， 交圓O於A、B。
(5)作∠CBA=∠B'，交圓O於C。
(6)連AC，∠ABC即為求作的內接三角形。
證明：因弦AB和弦EF同與圓O (小)相切，知弦，AB= EF, 則∠C=∠D=∠C'；據作圖∠B=∠B’，故知△ABC∽△A'B'C'，則知BC:AC:AB= B'C':A'C':A'B'=a:b:c。△ABC符合作圖要求。
討論:本題因P點落在內接三角形的哪一個邊上，並沒有規定，且P點在內接三角形一邊上的位置又有所不同，故解數可以較多。為了便於討論，設△ABC (或△A'B'C'的一相似內接三角形)三邊的弦心距分別為 。其解數情況如下:
(1)不符合條件 時，無解；
(2)符合上述條件時，
①當d1>OP、d2>OP、d3>OP，無解;
②當d1>OP、d2>OP、d3=OP，有一解，
③當d1>OP、d2>OP、d3<OP，有二解，
④當d1>OP、d2=OP、d3<OP，有三解;
⑤當d1>OP、d2<OP、d3<OP，有四解;
⑥當d1=OP、d2<OP、d3<OP，有五解;
⑦當d1<OP、d2<OP、d3<OP，有六解。
