清宮定理,幾何著名定理之一,由日本數學家清宮俊雄(Toshio Seimiya)提出。
設P、Q為△ABC的外接圓上異於A、B、C的兩點,P關於三邊BC、CA、AB的對稱點分別是U、V、W,且QU、QV、QW分別交三邊BC、CA、AB或其延長線於D、E、F,則D、E、F在同一直線上.
基本介紹
- 中文名:清宮定理
- 提出者:清宮俊雄
- 套用學科:數學
- 適用領域範圍:圓與直線的計算
清宮定理,證明,
清宮定理
證明
P、Q兩點和D、F、E、三點有如下關係:
將三角形的三邊或者其延長線作為鏡面,則從P點出發的光線照到D點經過BC反射以後通過Q點,從P點出發的光線照到E點經AC的延長線反射後通過Q點,從P點出發的光線照到F點後通過Q點
我們決定將證明清宮定理的方針確定如下:因為D、E、F三點中,有兩點在△ABC的邊上,其餘一點在邊的延長線上,
如證明
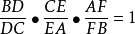
則根據梅涅勞斯定理的逆定理,就可證明DEF三點在同一直線上。
首先,A、B、P、C四點共圓,因此
∠PCE=∠ABP
但是,點P和V關於CA對稱
所以∠PCV=2∠PCE
又因為P和W關於AB對稱,所以
∠PBW=2∠ABP

從這三個式子,有
∠PCV=∠PBW
另一方面,因為∠PCQ和∠PBQ都是弦PQ所對的圓周角,所以
∠PCQ=∠PBQ
兩式相加,有
∠PCV+∠PCQ=∠PBW+∠PBQ
即∠QCV=∠QBW
即△QCV和△QBW有一個頂角相等,因此
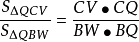
但是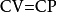 ,
,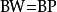 ,所以
,所以
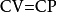
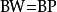
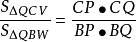
同理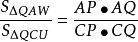
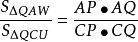
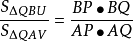
於是
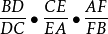
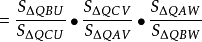
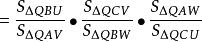
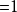
根據梅涅勞斯定理的逆定理,D、E、F三點在同一直線上

