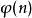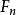法雷級數,是指每一行從0/1開始,以1/1結尾,其它數自左至右將所有的真分數按增加順序排列;第n行是由所有分母小於或等於n的真分數組成,我們稱為n階法雷級數。
基本介紹
- 中文名:法雷級數
- 外文名:Farley number column
- 名詞類型:定義概念
- 名詞領域:數學
- 書籍:《數學中的智巧》
- 別名:法里數列、法里級數
法雷級數定義,1、定義,2、第n行Fn的真分數的個數有多少個,數列長度,性質,福特圓,
法雷級數定義
1、定義
R.亨斯貝爾格著李忠翻譯的《數學中的智巧》一書,介紹了法雷級數。
如下表:
F1:0/1 1/1
F2:0/1 1/2 1/1
F3:0/1 1/3 1/2 2/3 1/1
F4:0/1 1/4 1/3 1/2 2/3 3/4 1/1
F5:0/1 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 1/1
F6:0/1 1/6 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 5/6 1/1
…… ………………………………
2、第n行Fn的真分數的個數有多少個
我們設Fn的個數為ψ(n), ψ(n)比 ψ(n-1)增加的個數是分母是n,分子比n小且與n互質的數的個數,這正是歐拉函式φ(n)。即
ψ(n)=ψ(n-1)+ φ(n).
ψ(1)=1+φ(1).
ψ(2)=ψ(1)+φ(2).
ψ(3)=ψ(2)+φ(3).
………………
ψ(n)= ψ(n-1)+ φ(n).
所以 ψ(n)=1+φ(1)+φ(2)+φ(3)+……+φ(n)很容易證明,當n≥3時,歐拉函式φ(n)是個偶數。由此我們得到除ψ(1)=2是偶數外,法雷級數其它各級的個數都是奇數,並且許多是素數。ψ(1)=2,ψ(2)=3,ψ(3)=5,ψ(4)=7,ψ(5)=11,ψ(6)=13,ψ(7)=19,ψ(8)=23,ψ(9)=29,……。
數列長度
n階的法里數列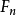 包含了較低階的法里數列的全部項,特別是它包含
包含了較低階的法里數列的全部項,特別是它包含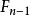 的全部項,和與n互質的每個數的相應分數。所以
的全部項,和與n互質的每個數的相應分數。所以 包含了
包含了 和分數1⁄6及5⁄6。對大於1的n,其法里數列的中間項必定是1⁄2。
和分數1⁄6及5⁄6。對大於1的n,其法里數列的中間項必定是1⁄2。
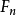
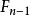



從 這項資料,可以推導出
這項資料,可以推導出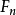 的長度公式:
的長度公式:

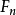
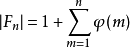

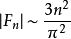
性質
法雷級數Fn具有很多美妙的性質,下面是一些常見的性質:
1.如果a/b,c/d是相鄰的兩項,則abs(a*d-b*c)=1。
2.如果a/b,c/d,e/f是相鄰的三項,則 (a+e)/(b+f)=c/d,特別的,如果c/d是新添加的,即c/d不屬於F(n-1),則c=a+e;d=b+f。
關於Farey級數的介紹。根據這條性質可以知道,叢F(n−1)到F(n)的構造過程中,F(n)的新項的分母一定是其相領兩項的分母和。另一方面,如果F(n−1)中的相鄰兩項 a/b,c/d, b+d=n,則(a+c)/n一定會被添加到F(n)中。
福特圓
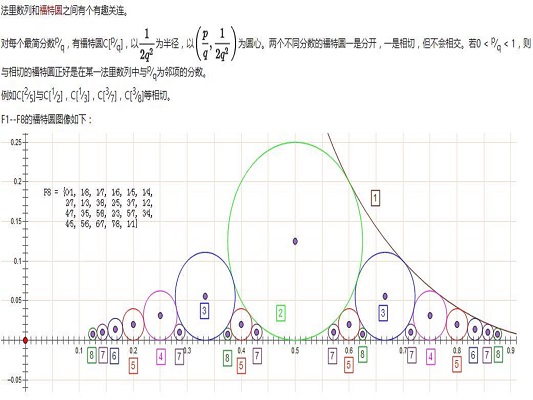
法里數列和福特圓之間有個有趣關連。
對每個最簡分數p⁄q,有福特圓C[p⁄q],以為半徑,以 為圓心。兩個不同分數的福特圓一是分開,一是相切,但不會相交。若0<p ⁄q<1,則與相切的福特圓正好是在某一法里數列中與p⁄q為鄰項的分數。
為圓心。兩個不同分數的福特圓一是分開,一是相切,但不會相交。若0<p ⁄q<1,則與相切的福特圓正好是在某一法里數列中與p⁄q為鄰項的分數。

例如C[2⁄5]與C[1⁄2],C[1⁄3],C[3⁄7],C[3⁄8]等相切。
F1--F8的福特圓圖像如圖1:
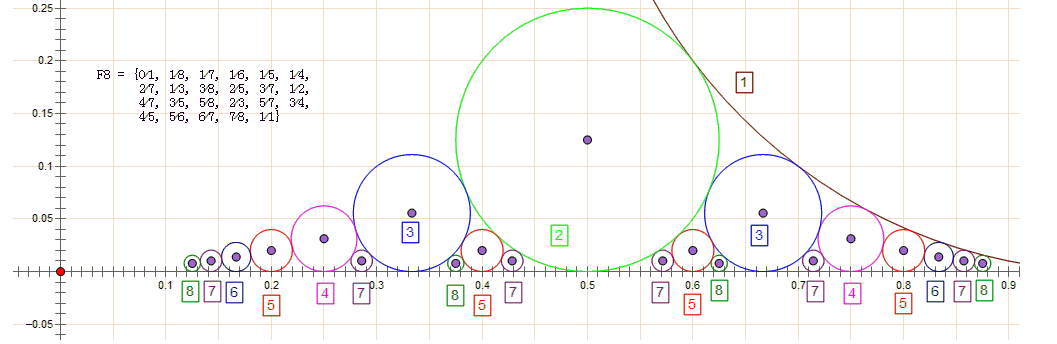 圖1 福特圖像
圖1 福特圖像