歸約是使用解題的"黑盒"來解決另一個問題的思維方式。歸約讓我們理解兩個問題間的關係,它是一種技術,用於尋找解決某個問題或它的變形。
基本介紹
- 中文名:歸約
- 外文名:Reduction
- 套用:假設有一個複雜的問題P
- 定義:決其它問
- 性質:思維方式
- 屬於:一種技術
概述,複雜性類的判別,套用,結論,
概述
我們解題時常遇見似曾相識的題目。此時,我們若可將新題轉換成已解舊題的一例,則新題亦解矣。
另一更微妙的用法是:若我們擁有一個已證明難以解決的問題,我們又獲得另一個相似的新問題。我們可合理推想此新問題亦是難以解決的。我們可由下列謬證法得證:若此新問題本質上容易解答,且若我們可展示每箇舊問題的實例可經由一系列轉換步驟變成新問題的實例,則舊問題便容易解決,因此得到悖論。因此新問題可知亦難以解決。
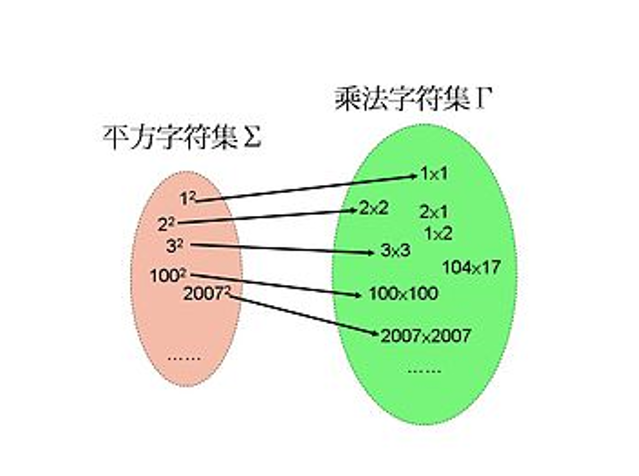
一個歸約簡例是從乘法化成平方。構想我們僅能以加、減、平方與除以二等操作,我們可運用此知識並結合下列方程式,以取得任兩數的乘積:
- a×b= ((a + b)2- a2- b2)/2.
我們亦可從另一方向歸約此問題:顯然地,若我們可以乘以任兩數,則我們可以對任一數平方:
- a=a×a.
因此可見兩問題之難度似乎相等,此類歸約稱為圖靈歸約。
然而,若我們增加條件:“此運算只能使用平方一次,且只能在結尾使用”,則更難尋找合適歸約。在這條件下,即使我們使用所有基礎運算,包括乘法,也找不到適當的歸約步驟。因為我們不僅要運算有理數,也必須運算像是根號2的無理數。而另一方向的歸約,我們的確可用一次乘法簡單地平方任何數,且此乘法的確是最後的運算。將此限制形式導入歸約中,我們已展示其歸約結論:普遍來說,乘法的確難於平方。此歸約稱為多一歸約。
複雜性類的判別
- 若要證明一問題是不可在決定的,我們可以一可計算函式將它轉換成另一已知不可決定的問題,例如,欲證P是不可決定的,可試將停機問題化約成問題P。
- 複雜度類P、NP與PSPACE擁有多項式時間歸約的封閉性。
- 複雜度類L、NL、P、NP與PSPACE擁有對數空間歸約的封閉性。
套用
在計算複雜度中,主要有兩大類的歸約:多一歸約與圖靈歸約。多一歸約將一問題的所有實例對應到另一問題的實例上;圖靈歸約計算一問題的解,並假設其他問題容易解決。多一歸約弱於圖靈歸約。較弱的歸約在分割問題的種類上效率較高,但它們的威力較弱,使本類歸約較難設計。
然而,為了使歸約有用,它們必須易於使用。例如實際研究中常常要將難以得解的NP完備問題,例如SAT問題,歸約成顯而易懂的問題,像藉由效率為指數時間並在有解時輸出整數零的機器,決定一數是否為零。但這並沒有多少用處,因為我們可以執行如同解決舊問題一樣難的歸約以解決新問題。
因此,依照複雜度類別使用適當歸約符號的學問興起。在鑽研複雜度類NP與更難的類別時,我們使用多項式時間多一歸約。在多項式階層中定義類別時,我們使用多項式時間圖靈歸約。當我們在類別P之內學習NC與NL類別時,我們使用對數空間歸約。歸約也用在可計算性理論中,以顯示問題是否可不可被任何機器解決;在此情境下,歸約僅局限於可計算函式上。
假設有一個複雜的問題P,而它看起來與一個已知的問題Q很相似,可以試著在兩個問題間找到一個歸約(reduction, 或者transformation)。
對於問題的先後,歸約可以達到兩個目標:
(1)已知Q的算法,那么就可以把使用了Q的黑盒的P的解決方法轉化成一個P的算法。
(2)如果P是一個已知的難題,或者特別地,如果P的下限,那么同樣的下限也可能適用於Q。前一個歸約是用於獲取P的信息;而後者則是用於獲取Q的信息。
結論
歸約讓我們理解兩個問題間的關係,它是一種技術,用於尋找解決某個問題或它的變形。