基本介紹
- 中文名:標準摩爾熵
- 外文名:standard molar entropy
- 性質:化學名詞
- 學科:熱力學
體系的混亂度與熵,熱力學第三定律與物質的規定熵,化學反應的標準摩爾熵變,熵變和反應方向,
體系的混亂度與熵
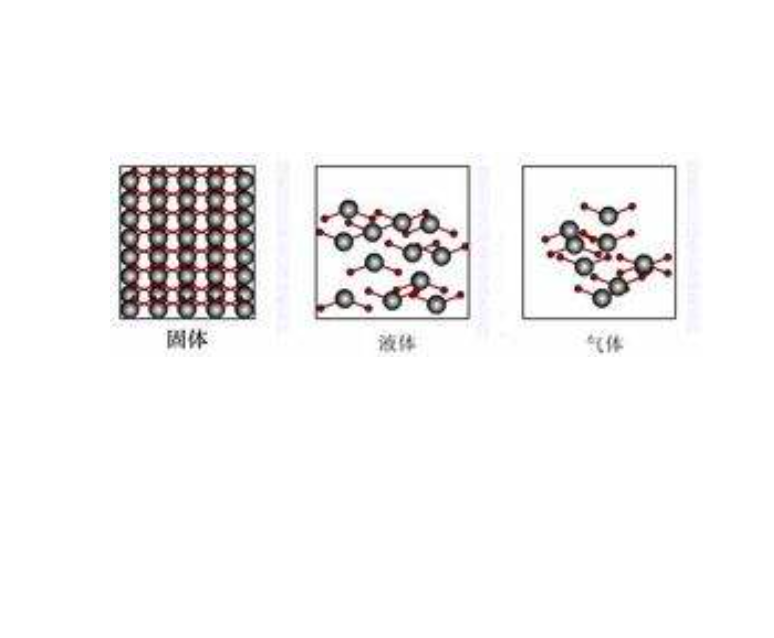
所謂體系的混亂度,就是指體系內部所有物質微粒(包括分子、原子、離子、電子、原子核、原子團,以及由這些基本粒子組成的更大的集合體、團粒等)所處狀態的混亂程度。這是與這些微粒的排列有序性相反的一個概念。 熵是人們用來描述、表征體系混亂度的函式。或者說,熵是體系混亂度的量度。體系的混亂度越大,熵值也越大,反之亦然。而體系的混亂度是體系本身所處的狀態的特徵之一。指定體系處於指定狀態時,其混亂度也是確定的,而如果體系混亂度改變了,則體系的狀態也就隨之有相應的改變。因此,熵也和熱力學能、焓等一樣,具有狀態函式的特性,熵也是一種狀態函式。
熱力學第三定律與物質的規定熵
熱力學第三定律有好幾種表述方法,這些表述方法字面上雖然各不相同,但其內容實質具有一定的聯繫和等效性。對熱力學第三定律的一種基本表述為:“不能用有限的手續把一個物體的溫度降到絕對零度”。而化學熱力學中最普遍採用的表述為:“在絕對零度時任何純物質的完整晶體的熵等於零”。這裡所謂完整晶體是指晶體中的原子或分子都只有一種排列形式。熱力學第三定律的內容與熵的概念是一致的。在絕對零度時,純物質的完整晶體中,所有的微粒都處於理想的晶格結點位置上,沒有任何熱運動,是一種理想的完全有序狀態,自然具有最小的混亂度,所以其熵值為零。根據熱力學第三定律So=0,利用熱力學的方法,熱化學測量,可以求得純物質的完整晶體從絕對零度加熱到某一溫度T的過程的熵變△S(T),(真正的完整晶體和絕對零度都是達不到的,實際上用在相當接近這一理想狀態的條件下得到的實驗結果外推後,用圖解積分的方法求得的)。
因為:△S(T)=ST—S0,而S0=0,所以ST=△S(T),即用上述方法測得的熵變△S(T),就等於在溫度T時,該物質的熵值,稱為該物質的規定熵。由此可定義:
在標準狀態下,1mol純物質的規定熵,即為該物質的標準摩爾規定熵,簡稱物質的標準熵。以Sm(-)表示,單位是J·K-1·mol-1。 應該注意,任一種穩定單質的規定熵和標準熵值都不為零。這是與物質的標準生成焓不同之處。
化學反應的標準摩爾熵變
對於化學反應而言,若反應物和產物都處於標準狀態下,則反應過程的熵變,即為該反應的標準熵變。當反應進度為單位反應進度時,反應的標準熵變為該反應的標準摩爾熵變,以△rSm(-)表示。與反應的標準焓變的計算相似,化學反應的標準摩爾熵變,可由生成物與反應物的標準熵求得。對於反應 aA+Bb=eE+dD,有
△rSm一(298k)=(eS m一(E)+ dH m一(D))-(aH m一(A)+ bH m一(B))
例3、 計算反應 203(g)=302(g)在298K時的△rSm一。
【解】 查表得 Sm(-)(O2,g)=205.1 J·mol-1·K-1