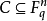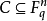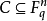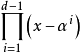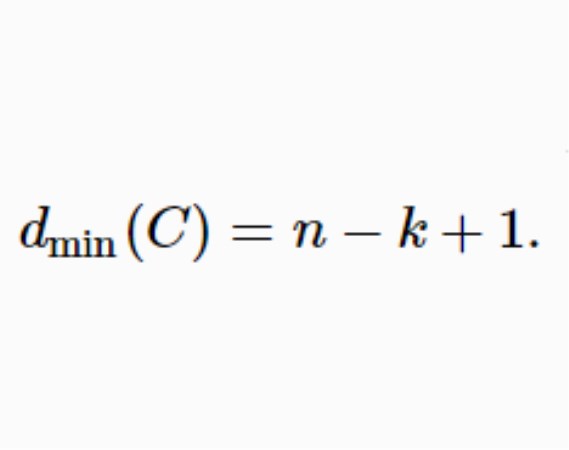極大距離可分碼(maximum distance separable code)亦稱MDS碼，指達到辛格爾頓界的碼。若M=qn+1-d，則稱q元(n，M，d)碼為極大距離可分碼，當n-d+1=2時，q元(n，q2，d)MDS碼的存在性等價於n-2個q階相互正交拉丁方的存在性，當C為[n，k，d]線性碼時，C為MDS碼的充分必要條件為d=n-k+1，MDS線性碼有許多有趣的性質，例如，MDS線性碼的對偶碼也是MDS碼，一個[n，k，d]線性碼是MDS碼的充分必要條件為生成矩陣中任意k列均線性無關，此外，若在射影幾何PG(k-1，q)中存在n個點的集合S使其中沒有k個點位於同一個超平面內，則存在一個[n，k，d]MDS碼。
基本介紹
- 中文名：極大距離可分碼
- 外文名：maximum distance separable code
- 簡稱：MDS碼
- 簡介：達到辛格爾頓界的碼
- 所屬學科：數學（組合設計）
基本介紹,相關介紹,極大距離可分碼舉例,
基本介紹
定理1辛格爾(Singleton)頓界 設
是一個參數為[n,k]的線性碼，則C的極小距離d≤n-k+1。
以上表明一個線性碼的極小距離不會“太大”，無論怎樣努力，都不能夠構造出一個參數為[n,k]的線性碼，使得它的極小距離大於n-k+1，由此可見，最好的期望就是構造使得極小距離等於n-k+1的線性碼，於是引出下面的定義。
一個參數為[n,k]的線性碼C，若滿足dmin(C)=n-k+1，則稱該碼為極大距離可分碼，簡稱為MDS碼。
事實證明，MDS碼是存在的，下面廣義Reed-Solomon碼就是MDS碼。
相關介紹
證明定理1之前先介紹一個定理，下面的定理揭示了線性碼的校驗矩陣與其極小重量亦即極小距離之間的關係。
定理2設 是一個參數為[n,k]的線性碼，令u∈C，WH(u)=m，C的校驗矩陣為H,則H中有m列存在一個線性相關關係。反之，對於H的m列中任何一個線性相關關係，都對應一個C中重量不大於m的碼字。
證明：因為u∈C，H是C的校驗矩陣，所以HuT=0，又WH(u)=m，去掉u的零分量，這正是H的m列的一個線性相關關係。因此，H中有m列存在一個線性相關關係。反之，如果H的m列有一個線性相關關係，則存在m個不全為零的係數，使得這m列的線性組合等於零，現在定義一個一維行向量u：與這m個列對應的分量就取對應的這m個係數，其餘分量取零。顯然，WH(u)≤m,HuT=0，所以，u是一個C中重量不大於m的碼字。
推論1設 是一個線性碼，C的校驗矩陣為H，則C的極小重量亦即極小距離為d若且唯若d=max{m|H的任意m-1列都線性無關}。
證明:由定理2可得。
定理1的證明：設參數為[n,k]的線性碼C的校驗矩陣為H,則H是一個秩為n-k的(n-k)×n矩陣，因此，H中的任意n-k+1列都線性相關。由定理2可知，
d≤n-k+1。
極大距離可分碼舉例
Reed-Solomon碼 一個Reed-Solomon碼(RS碼)是Fq上長為n=q-1的本原BCH碼，這種碼的生成元具有形式g(x)=
，其中α是Fq的一個本原元。
下述定理3的系理實際上就是說Reed-Solomon碼是極大距離可分碼。
定理3設計距離d的碼長q-1的q元Reed-Solomon碼的極小距離等於d.。
系理 設計距離d的碼長n=q-1的q元Reed-Solomon碼的碼長n，信息位的個數k和極小距離d三者之間適合關係式：
d=n-k+1.
注意，一般說來，我們有：
定理4 (n，k)線性碼的極小距離d≤n-k+1。
