極大商環(maximal ring of quotients)是一種特殊的商環。
基本介紹
- 中文名:極大商環
- 外文名:maximal ring of quotients
詹森(Johnson, R. E.)和內海(Utumi,Y.)從環的稠密左理想到環自身的模同態出發構造的一種分式(商)環.設R是有1環,必是含一切序對(D,a)的集合,其中,D是R的稠密左理想,a;DR是R模同態.在必中規定:(D, a)一(D', a',)若且唯若存在稠密左理想D D門D',使得a , a'在刀‘上一致.於是,“一”是中的等價關係,從而決定中的一個分類.若D,司表示(D, a)所在的等價類,Q,., ( R)是一切等價類的集合,規定
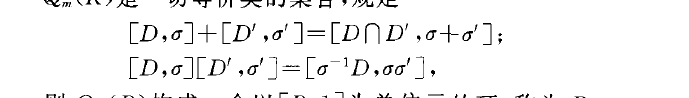
公式
則Q,., ( R)構成一個以[R,1]為單位元的環,稱為R的極大商環.對任意rER,若:二:R-R為右乘映射,則r-[R, r,]為R到Qn, ( R)的同構嵌人,即Q,n ( R含R為子環.上述方法是內海於1956年構造的.若R是奧爾環,則由R所構造的左全分式環QoR)里Q
,(R).
