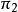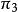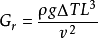格拉曉夫數(Gr)是流體動力學和熱傳遞中的無量綱數,其近似於作用在流體上的浮力與粘性力的比率。 在研究涉及自然對流的情況下經常出現,類似於雷諾數。 它被認為是以弗朗茨·格拉斯霍夫(Franz Grashof)命名的。 雖然這個術語組合已經被使用,但直到1921年,Franz Grashof去世後的28年,才被命名。
基本介紹
- 中文名:格拉曉夫數
- 外文名:Grashof number
- 別稱:升浮力數、格拉霍夫準數
- 縮寫:Gr
- 反映:自然對流程度的特徵數
- 表達式:Gr=gα△tl3/v2
簡介,推導,能量方程,白金漢姆定理,
簡介
格拉曉夫數(Gr)是流體動力學和熱傳遞中的無量綱數,其近似於作用在流體上的浮力與粘性力的比率。 在研究涉及自然對流的情況下經常出現,類似於雷諾數。 它被認為是以弗朗茨·格拉斯霍夫(Franz Grashof)命名的。 雖然這個術語組合已經被使用,但直到1921年,Franz Grashof去世後的28年,才被命名。 格拉曉夫數(又稱升浮力數或格拉霍夫準數)。
其公式為: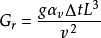
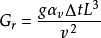
其中是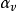 體積變化係數,對於理想氣體即等於絕對溫度的倒數,g是重力加速度,L是特徵尺度,Δt為溫差,分母是運動黏度的平方。
體積變化係數,對於理想氣體即等於絕對溫度的倒數,g是重力加速度,L是特徵尺度,Δt為溫差,分母是運動黏度的平方。
推導
推導格拉曉夫數的第一步是對體積展開係數進行如下操作:

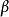

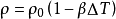
其中, 是體積流體密度;
是體積流體密度;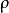 是邊界層密度。
是邊界層密度。

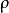

從這裡可以找到格拉曉夫數的兩種不同的方式。 一個涉及能量方程,而另一個包含由於邊界層和體液之間的密度差而引起的浮力。
能量方程
涉及能量方程的這個討論是關於旋轉對稱流動的。 該分析將考慮重力加速度對流動和熱傳遞的影響。 要遵循的數學方程既適用於旋轉對稱流動又適用於二維平面流動。

s是旋轉方向,即平行於表面的方向
u是切向速度,即平行於表面的速度
y是平面方向,即垂直於表面的方向
v是正常速度,即垂直於表面的速度

在該方程中,上標n是區分來自平面流的旋轉對稱流。 這個方程的以下特徵成立。
n = 1:旋轉對稱流
n = 0:平面,二維流
g是重力加速度
隨著物理流體性質的增加,該方程式擴展到以下內容:
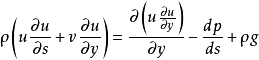

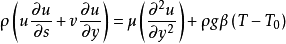
動量方程的進一步簡化來自於體積膨脹係數,密度關係 和運動粘度關係
和運動粘度關係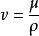 ,進入動量方程。
,進入動量方程。

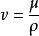
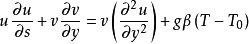

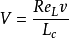


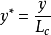
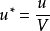
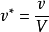



其中,
是表面溫度
是體積流體溫度

上述方程中括弧中的無量綱參數稱為格拉曉夫數:
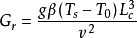
白金漢姆定理
將導致格拉曉夫數的另一種形式的維度分析稱為白金漢姆定理。由於邊界層和體積流體中的密度差異,該方法考慮了每單位體積的浮力力 。
。

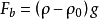

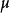
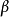

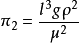
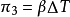
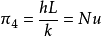
通過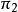 和
和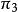 ,我們得到格拉曉夫數:
,我們得到格拉曉夫數: