柳卡圖,也稱為折線圖,可以很好的解決複雜的行程問題。快速的解法是直接畫時間-距離圖,再畫上密密麻麻的交叉線,按要求數交點個數即可完成。折線示意圖往往能夠清晰的體現運動過程中“相遇的次數”,“相遇的地點”,以及“由相遇的地點求出全程”,使用折線示意圖法一般需要我們知道每個物體走完一個全程時所用的時間是多少。
基本介紹
- 中文名:柳卡圖
- 別名:折線圖
- 適用範圍:行程問題
- 分類:迎面相遇、追及相遇
社會評價,
社會評價
多次相遇行程問題的必備工具——柳卡圖
其中“相遇”兩字廣義上講,只要兩人在同一地點就算相遇,因次分為兩種情況,一種叫做迎面相遇(即我們平時說的相遇問題),一種應鞏朽叫做追及相遇(即我們平時說試譽章的追及問題),一般題目說的相遇,我們默認指的是迎面相遇,若題目說只要兩人拔喇懂在同一地點算做一次相遇,那么這時兩種情況都要算。
以下舉兩個例子:
【例1】 甲、乙兩人在一條90米的直路上來回跑步,甲的速度3米/秒,乙的速度2米/秒。如果他們同時分別從直路的兩端A、B兩點出發,當他們跑12分鐘,共相遇了多少次?(從出發後兩人同時淚連良歸到達某一點算作一次相遇)。
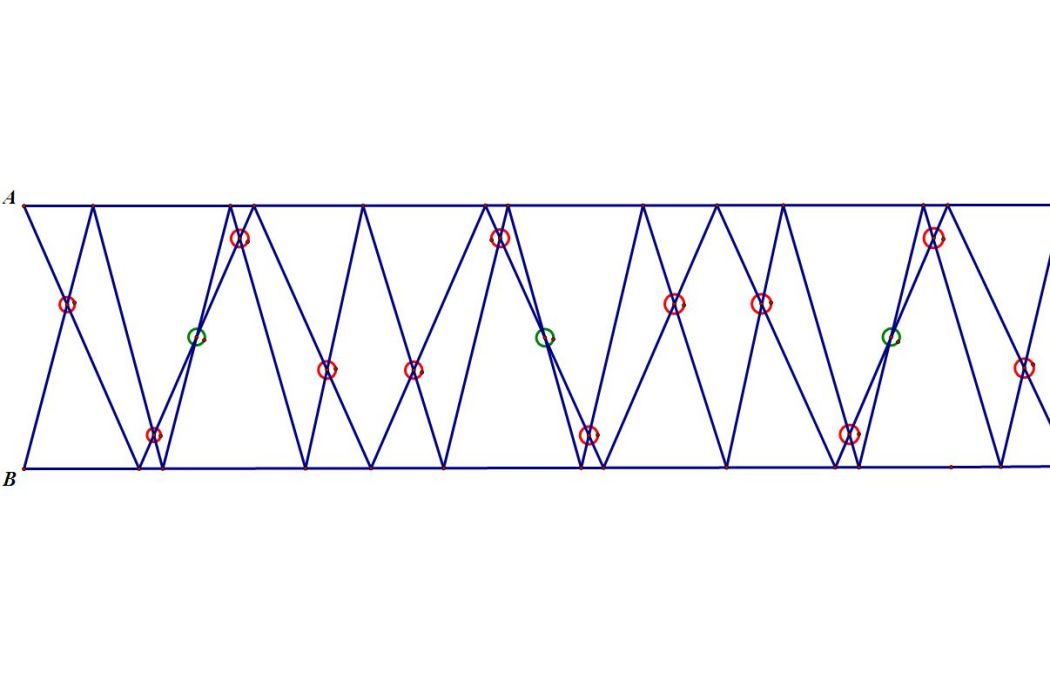
【分析】 多次相遇,如圖1所示,甲用實線表示,乙用虛線表示
在180秒內,甲、乙共相遇5次,最後又回到出發的狀態。
所以甲、乙共相遇了[12÷(180÷60)]×5=20(次)
【例2】甲、乙兩訂說匙人在一條長為30米的直路上來回跑步,甲的速度是每秒1米,乙的速度是每秒0.6米.如果他們同時分別從直路的兩端出發,當他們跑了10分鐘後,共相遇幾次?
首先,甲跑一個全程需要30÷1=30(秒),乙跑一個全程需要30÷0.6=50(秒).與上題類似,畫運行圖如下(實線表甲,虛線表示乙,那么實虛兩線交點就是甲乙相遇的地點):
從圖1中可以看出,當甲跑5個全程時,乙剛好跑3個全程,各自到了不同兩端又重新開始,這正好是一周期150秒.在這一周期內兩人相遇了5次,所以兩人跑10分鐘,正好是四個周期,也就相遇5×4=20(次)
備註:一個周期夜台棗員內共有5次相遇,其中第拜拔1,2,4,5次是迎面相遇,而第3次是追及相遇