東西距又叫橫距,是起航點和到達點兩經度線間所夾中分緯度圈的弧長。東西距常以海里為單位。起航點和到達點的經差不能直接求出,可利用東西距間接換算為經差。
基本介紹
- 中文名:東西距
- 外文名:Departure
- 符號:Dep
- 單位:海里
- 作用:可利用東西距求得經差
- 本質:兩點經度線間所夾中分緯度圈弧長
中分緯度圈

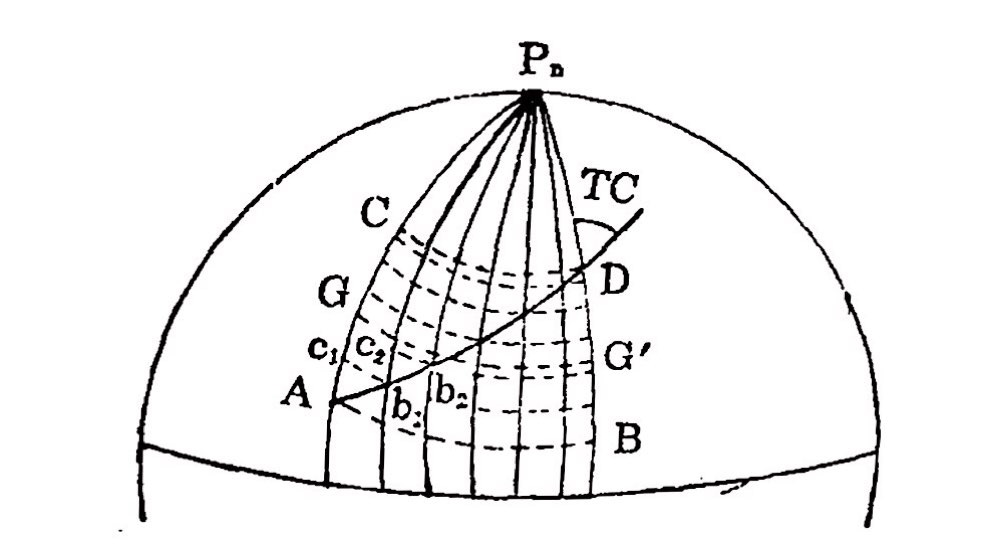

簡介
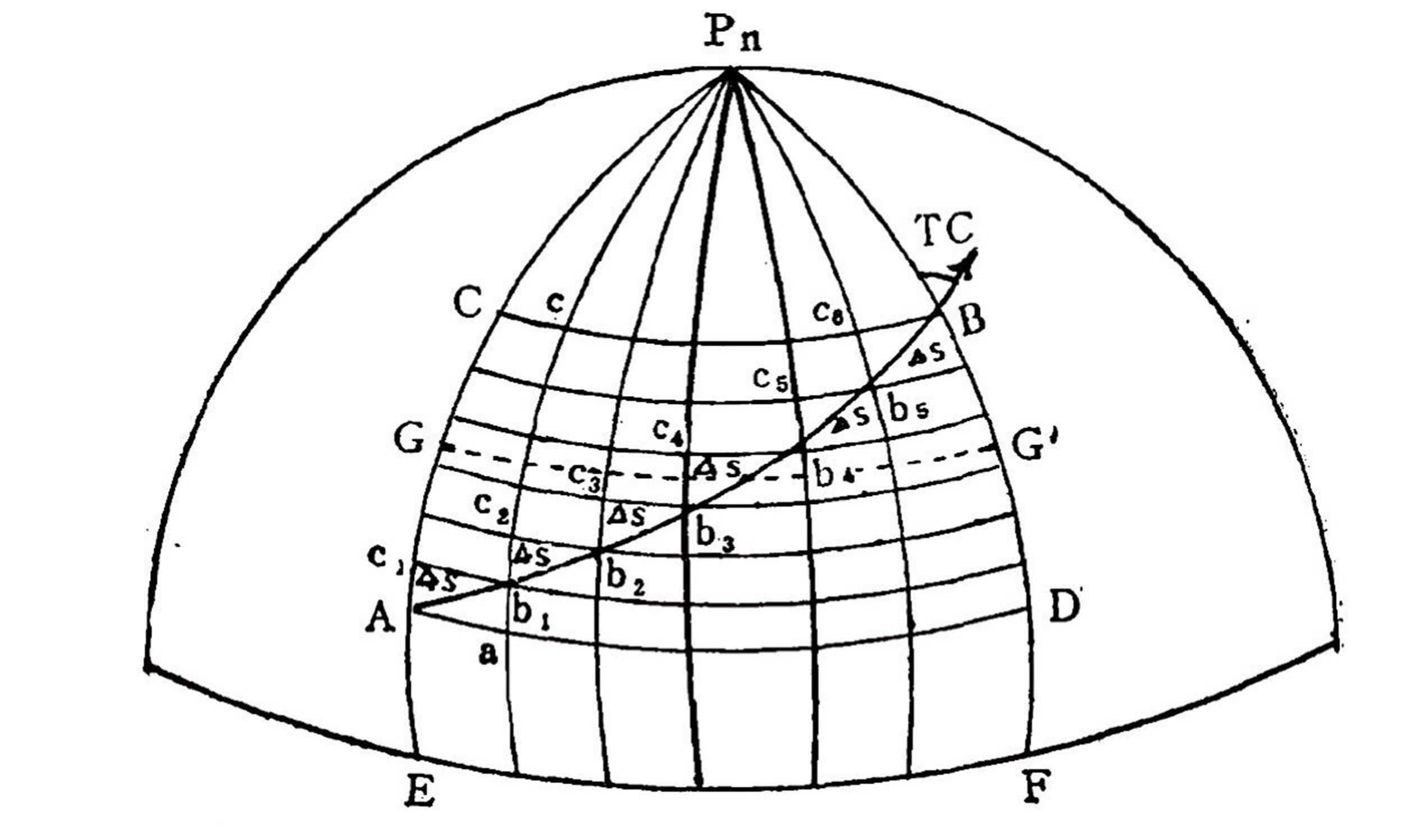
計算公式
















東西距與經差








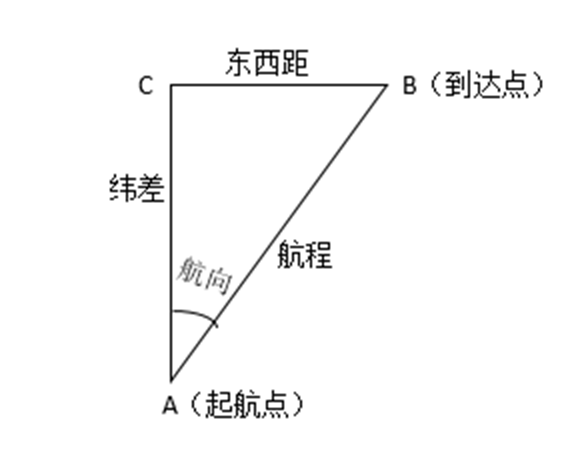
東西距又叫橫距,是起航點和到達點兩經度線間所夾中分緯度圈的弧長。東西距常以海里為單位。起航點和到達點的經差不能直接求出,可利用東西距間接換算為經差。




























東西距又叫橫距,是起航點和到達點兩經度線間所夾中分緯度圈的弧長。東西距常以海里為單位。起航點和到達點的經差不能直接求出,可利用東西距間接換算為經差。中分緯度圈中分緯度圈是介於起航點所在緯度圈和到達點所在緯度圈的一個假想緯...
東西dōngxī [East and west]∶東面和西面東西植松柏。——《玉台新詠·古詩為焦仲卿妻作》[From east to west]∶從西到東的距離縱有健婦把鋤犁,禾生隴畝無東西。——唐· 杜甫《兵車行》中國東西有5000公里 [Four directions of north,south,west and east]∶泛指四方叫囂乎東西。——唐· 柳宗元《捕...
所以,只要記住準星遮蓋目標的情況,就能立即估出距離來。方法四:用指北針測 指北針不但能給東西南北方向,還能告訴你到目標的距離。工廠在設計製造指北針時,就已經考慮到用它測量距離的問題了。打開指北針,你馬上就能發現有準星、照門。準星座兩側尖端的寬度恰好是準星座到照門距離的十分之一。準星座就是估計判定...
距離度量是數學中的法則,用在某些空間中測量沿曲線的距離和曲線間的角度,包含曲線所在空間的曲率的信息。距離是數學中的法則,用在某些空間中測量沿曲線的距離和曲線間的角度,包含曲線所在空間的曲率的信息。這是廣義相對論的中心主題。廣義相對論建立了表示距離度量(因而也是曲率)與物質分布關係的方程。對於數字...
距離測量是指測量地面上兩點連線長度的工作。通常需要測定的是水平距離,即兩點連線投影在某水準面上的長度。它是確定地麵點的平面位置的要素之一。是測量工作中最基本的任務之一。通常需要測定的是水平距離,即兩點連線投影在某水準面上的長度。在三角測量、導線測量、地形測量和工程測量等工作中都需要進行距離測量。
注意值得你注意,學習值得你學習的東西足矣。距離產生美 每天和你在一起時間最長的人是你的同事。同事關係好,團結互助可以,但是切記同事之間拒絕親密。同事就是同事,不是朋友,交朋友,除了志趣相投外,忠誠的品格是最重要的,彼此信任、忠實於友誼是雙方的責任。同事則不同,一般來說,如果不是自己創的業,也不...
水星東大距是指水星與太陽的距角達到最大,且在太陽的東邊。水星在太陽東邊稱水星東大距,在太陽西邊稱水星西大距。水星東大距時,可以在黃昏時分西方地平線上找到水星;“水星西大距”時,水星則在黎明時東方低空出現。但真正要在大距時看到水星,還需要日落或日出時水星儘可能位於太陽的正上方。水星的最大距角...
光山縣,在州城西南四十里。東西距一百五里,南北距二百里。東至本州界二十里,西至汝寧府羅山縣界八十五里,北至息縣界八十里,東南至商城縣界七十里,西南至湖北黃州府黃安縣界一百八十里,東北至本州界二十里,西北至息縣治九十五里。固始縣,在州城東一百四十里。東西距一百二十里,南北距一百二十里。東至...
距,漢語一級字,讀作距(jù),注音是ㄐㄩˋ,部首是足,本義指雞爪。 現代釋義 基本字義 距jù ⒈ 相隔的空間和時間:相距數里。距離。行(háng )距。株距。差(chā)距。⒉ 雄雞爪子後面突出像腳趾的部分。⒊ 古同“拒”,抵抗。⒋ 古同“巨”,大。基本詞義 ◎ 距 jù 〈名〉(1) (形聲。從...
大距是指地內行星(就是水星和金星)從地球上看上去離太陽最遠的一點。東大距,從地球上看距離太陽最遠時水星(或金星)在太陽東邊。東大距時,可以在黃昏時分的西方地平線上方找到水星。2018年3月15日,水星上演過東大距。2024年7月22日,水星迎來2024年的第四次大距,也是第二次東大距。形成原因 對於水星...
此部位有高的建築物或廁所、淨化槽等東西存在的話,就是凶。同時,潮濕也不好。主屋與輔助建築也要有一點距離才好,或變成三合關係也可以。如果過於靠近主屋或影子遮到主屋,也是兇相。西方位 這個部位在一天中,是表示工作完畢後,休息的時間,在季節上意味著在初秋時得到陰氣的培養,而變成有形的收穫,即迎接...
水星西大距指水星出現在太陽西邊。由於距離太陽太近,水星經常湮沒在太陽的光輝中,每年只有數次短暫的可觀測機會,從而成為太陽系八大行星中最難觀測到的一顆。只有等到水星和太陽的角距達最大即“大距”時,公眾才最有希望目睹水星。水星在太陽東邊稱“東大距”,在太陽西邊稱“西大距”。“東大距”時,可以在...
金星東大距是指金星在太陽的東面,同時從地球看去,金星與太陽的張角最大。當一顆內側行星在日落後能看見時,它通常是接近東大距,而在日出之前能看見時,則是接近西大距的時候。大距(東大距或西大距)的數值,對水星是在18° 和28°之間;對金星則是在45° 和47°之間。這個數值的變化是因為行星的軌道是...
距角是一個天文名詞,表示從地球上觀察時,行星和太陽之間分離的角度。 在天體周日視運動現象中,當天體有出沒時,如果Dec與φ同名且Dec>φ時,天體運行到其垂直圈與天體赤緯圈相切的切點時,該天體的方位角達到最大值,這時天體的位置稱為距角.當一顆內側行星在日落後能看見時,它通常是接近東大距,而在日出之前...
像距是像到平面鏡(或透鏡的光心)之間的距離·(物理中用v表示像距)像距口訣:一倍焦距分虛實 二倍焦距分大小 物近像遠像變大 物遠像近像變小 像距的實驗獲得 4.13-5。AB是物,A′B′是它的像,以xy作探針,放在平面鏡前調整位置,或者調整平面鏡的位置,使xy通過平面鏡成的像x′y′與A′B′無視差...
經距,是指固定緯圈的經向距離的簡稱,是為緯圈上的一段距離。由於緯圈上分為360等分,即為360個經度,而靠近赤道緯圈長度遠大於極地的緯圈長度,所以在赤道地區的一個經度的距離比極地要長的多。經距的計算方法 我們有必要先了解一下經緯度的確定:在地圖和地球儀上,我們可以看見一條一條的細線,有橫的,...
鏡頭焦距是指鏡頭光學後主點到焦點的距離,是鏡頭的重要性能指標。鏡頭焦距的長短決定著拍攝的成像大小,視場角大小,景深大小和畫面的透視強弱。鏡頭的焦距是鏡頭的一個非常重要的指標。鏡頭焦距的長短決定了被攝物在成像介質(膠片或CCD等)上成像的大小,也就是相當於物和象的比例尺。當對同一距離遠的同一個被攝...
不在同一高度上的兩點之間的距離即為斜距。簡介 如圖1所示。【平距】:是儀器與觀測點間的水平距離.斜距=平距÷俯視角的餘弦 【其它相關】:【水平角HA】:是兩觀測點之間的水角夾角=後視-前視。【天頂距】:在天體方位圈上,天體與天頂之間的角距離,稱之為天頂距。計算:它由測站點鉛垂線的天頂起算,由0...
經緯距 經緯距(plane rectangular coordinate)是1997年公布的鐵道科學技術名詞。公布時間 1997年,經全國科學技術名詞審定委員會審定發布。出處 《鐵道科學技術名詞》第一版。
當僅在一個方向上給定位置度公差時,公差帶是距離為公差值t,且以理想位置為中心對稱配置的兩平行直線(或兩平行平面)之間的區域,見圖冊3中的圖11和圖12。此時,公差帶的寬度方向是框格指引線箭頭所指的方向。當在兩個方向上給定位置度公差時,公差帶是正截面為公差值t1×t2,且以理想位置為軸線的四稜柱內的...
樓間距:兩相鄰樓的外牆面距離。同一個小區兩棟相鄰的樓與樓之間的距離。建築間距的控制是為了保障人們工作、生活的質量與安全,滿足必須的日照時長、採光、通風、隔音等要求。樓間距規定 按照國家規定(設計規範)以 冬至日照時間不低於1小時(房子最底層窗戶)為標準。間距是用建築物室外坪至房屋檐口的高度/tan(...
相距,讀音xiāng jù,漢語詞語,意思是彼此間距離。相隔;相互間距離。詞語解釋 1.對峙。距,通“拒”。2.相隔;相互間距離。運用示例 《史記·商君列傳》:“軍既相距,衛鞅遺魏將公子昂書。”《新五代史·雜傳四·趙犨》:“是時,梁將劉鄩等與莊宗相距澶魏之間,兵數敗。”宋·曾鞏《閬州張侯廟記...
視距測量是利用水準儀的望遠鏡內十字絲分劃板上的視距絲在視距尺(水準尺)上讀數,根據光學和幾何學原理,同時測定儀器到地麵點的水平距離和高差的一種方法。視距測量具有操作簡便、速度快、不受地面起伏變化的影響的優點,被廣泛套用於碎部測量中。但其測距精度低,約為:1/200-1/300。測量原理 水平視距 如圖(1...
軌距(rail gauge)是鐵路軌道兩條鐵軌(鋼軌)之間的距離(以鋼軌的內距為準)。現在全世界有多種不同的軌距,分為普軌、寬軌、窄軌。相同軌距可以有不同車身寬度高度,例如,中國標準軌道上的中國標準動車組比傳統列車寬一些、高一些、舒服一些。簡介 軌距(rail gauge)是鐵軌(鋼軌)頂面16mm範圍內兩股鋼軌作用...
雷射測距儀(Laser rangefinder),是利用調製雷射的某個參數實現對目標的距離測量的儀器。雷射測距儀測量範圍為3.5~5000米。按照測距方法分為相位法測距儀和脈衝法測距儀,脈衝式雷射測距儀是在工作時向目標射出一束或一序列短暫的脈衝雷射束,由光電元件接收目標反射的雷射束,計時器測定雷射束從發射到接收的時間,...
distance,英文單詞,名詞、動詞,作名詞時意為“距離;遠方;疏遠;間隔”;作動詞時意為“ 疏遠;把…遠遠甩在後面”。單詞發音 英[ˈdɪstəns]美[ˈdɪstəns]短語搭配 distance education遠程教育 ; 遙距教育 ; 遠程教學 ; 遠距教學 Hamming distance漢明距離 ; 海明距離 ; 漢娩距 ; 漢明距 ...
建築間距是指兩棟建築物外牆之間的水平距離,城市規劃特別是在詳細規劃中對建築間距有很嚴格的要求。技術原理 主要是根據日照(南北向建築)、通風、採光、防止噪聲和視線干擾、防火、防震、綠化、管線埋設、建築布局形式、以及節約用地,綜合考慮確定。住宅的布置,通常以滿足日照要求作為確定建築間距的主要依據。中華人民...
鋼尺量距,是指拿把鋼製的尺子去測量距離,量距方便,直接,且使用的工具成本低。特點介紹 鋼尺量距方便,直接,且使用的工具成本低; 視距測量利用經緯儀或水準儀望遠鏡中的視距絲和視距尺按幾何光學原理進行測距;磁波測距是用儀器發射及接收紅外光,雷射或微波等,按其傳播速度及時間確定距離。測量方法 一般方法 1、...
