將一個或多個有理數的值相加的過程叫有理數的加法,如:23+64+52=139、13.7+9.65+(-8)=15.35
有理數加法的運算結果必然是有理數。
分析理解,相關內容,加法解析,相加的例子,
分析理解
與國小加法的聯繫
有理數的加法與國小的加法大有不同,國小的加法不涉及到符號的問題,而有理數的加法運算總是涉及到兩個問題:一是確定結果的符號;二是求結果的絕對值.
法則理解
在進行有理數加法運算時,首先判斷兩個加數的符號:是同號還是異號,是否有0.從而確定用那一條法則.在套用過程中,一定要牢記"先符號,後絕對值",熟練以後就不會出錯了.
法則拓廣
多個有理數的加法,可以從左向右計算,也可以用加法的運算定律計算,但是在下筆前一定要思考好,哪一個要用定律哪一個要從左往右計算.
相關內容
法則
Ⅰ.同號兩數相加,取相同的符號,並把絕對值相加.
Ⅱ.異號兩數相加,絕對值相等時,和為零,絕對值不等時,取絕對值較大的數的符號,並用較大的絕對值減去較小的絕對值
Ⅲ.一個數與0相加,仍得這個數.
運算律
有理數的加法同樣擁有交換律和結合律(和整數得交換律和結合律一樣)用字母表示為:
交換律:a+b=b+a
結合律:(a+b)+c=a+(b+c)
要點
同號相加不變,異號相加變減.欲問符號怎么定,絕對值大號選.
在進行有理數加法運算時,一般採取:1.是互為相反數的先加(抵消);2.同號的先加;3.同分母的先加;4.能湊整數的先加;5.異分母分數相加,先通分,再計算.
記憶口訣
有理加法不含糊
同號異號分清楚
如果兩數號相同
絕對相加號相從
如果兩數號相異
大絕來把小絕去
結果符號大絕替
加法解析
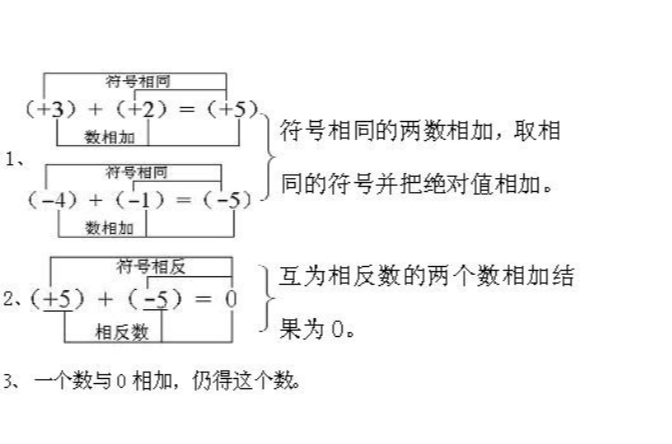
一般地,同號兩數相加有下面的法則:
同號兩數相加,取與加數相同的符號,並把絕對值相加。
一般地,異號兩數相加有下面的法則:
異號兩數相加,取絕對值較大的加數的符號,並用較大的絕對值減去較小的絕對值。
另外,有理數相加還有以下法則:
互為相反數的兩個數相加得零;一個數同零相加,仍得這個數。
相加的例子
兩個有理數相加,有多少種不同的情形?
為此,我們來看一個大家熟悉的實際問題:
足球比賽中贏球個數與輸球個數是相反意義的量.若我們規定贏球為“正”,輸球為“負”,打平為“0”.比如,贏3球記為+3,輸1球記為-1.學校足球隊在一場比賽中的勝負可能有以下各種不同的情形:
(1)上半場贏了3球,下半場贏了1球,那么全場共贏了4球.也就是
(+3)+(+1)=+4.
(2)上半場輸了2球,下半場輸了1球,那么全場共輸了3球.也就是
(-2)+(-1)=-3.
那么,請同學們說出其他可能的情形.
答:上半場贏了3球,下半場輸了2球,全場贏了1球,也就是
(+3)+(-2)=+1;
上半場輸了3球,下半場贏了2球,全場輸了1球,也就是
(-3)+(+2)=-1;
上半場贏了3球下半場不輸不贏,全場仍贏3球,也就是
(+3)+0=+3;
上半場輸了2球,下半場兩隊都沒有進球,全場仍輸2球,也就是
(-2)+0=-2;
上半場打平,下半場也打平,全場仍是平局,也就是
0+0=0.
上面我們列出了兩個有理數相加的7種不同情形,並根據它們的具體意義得出了它們相加的和.但是,要計算兩個有理數相加所得的和,我們總不能一直用這種方法.現在請同學們仔細觀察比較這7個算式,你能從中發現有理數加法的運算法則嗎?也就是結果的符號怎么定?絕對值怎么算?
1.同號兩數相加,取相同的符號,並把絕對值相加;
2.絕對值不相等的異號兩數相加,取絕對值較大的加數符號,並用較大的絕對值減去較小的絕對值,互為相反數的兩個數相加得0;
3.一個數同0相加,仍得這個數.