有形數

有形數是可以排成有一定規律形狀的數。有形數是畢達哥拉斯學派的關注重點之一，他們認為數和形有不可分割的關係。

基本介紹

• 中文名：有形數
• 定義：可以排成有一定規律形狀的數
• 地位：畢達哥拉斯學派的關注重點之一
• 種類：多邊形數、多面體數等

概述

有形數是可以排成有一定規律形狀的數。有形數是畢達哥拉斯學派的關注重點之一，他們認為數和形有不可分割的關係。有形數都是自然數，它們可以用小石子堆砌。有形數是將數形象化的方法。一般地，任意一個自然數都可以表示為m個m邊形數地和。

有形數 - 種類

有形數可依照該數能排成的形狀分成:

多邊形數、多面體數、中心多邊形數、中心多面體數、星數、角錐數、角柱數、多胞體數.......等。

有形數 - 例子

有形數三角形數

能排成三角形的有形數

前17個三角形數是1、3、6、10、15、21、28、36、45、55、66、78、91、105、120、136、153……（OEIS中的數列A000217）

梯形數

能排成梯形的有形數

前15個梯形數為2, 7, 15, 26, 40, 57, 77, 100, 126, 155, 187, 222, 260, 301, 345......（OEIS中的數列A005449）

中心五邊形數梯形數公式：（頂層數+底層數）×層數÷2

中心五邊形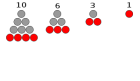數

中心五邊形數

排成從中心延伸出去的五邊形

前15項的中心五邊形數為1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526......（OEIS中的數列A005891）.

四角錐的有形數四角錐數

能堆成四角錐的有形數

四角錐的有形數

前13個四角錐數是1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819...... （OEIS中的數列A000330）.

六角星數

能排成六角星的有形數

前13個六角星數是1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, 937......（OEIS中的數列A003154）

四角錐的有形數