最小費用流問題

定義

在一個網路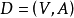

中，弧

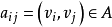有容量上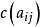界

和下界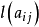

，即單位流量的費用

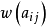。另外，每一個頂點

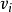都有一個貨物供需量

：

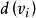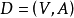
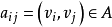
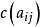
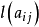
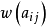
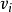
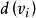
當它大於0時，表示該點可供給一定量的貨物；

當它小於0時，表示該點需求一定量的貨物；

當它為0時，表示該點既不需要也不能提供貨物，這樣的點可以作為貨物的中轉點。

另外，假設網路中供需是平衡的。

網路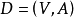

中的一個可行流是滿足以下流量守恆和約束條件的函式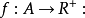

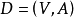
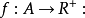
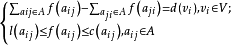
最小費用流問題是求一個可行流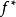

使其費用最小，即

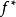
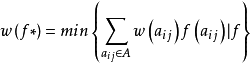
該問題存在多項式時間算法。

[polynomial-time algorithm]

若一個算法的計算時間不超過其所求解問題的輸入長度的一個多項式，則稱該算法為多項式時間算法；其中計算時間和輸入長度是以確定性圖靈機為計算模型。通常認為只有多項式時間算法是可以求解大規模的實際問題，故多項式時間算法也稱好算法或者有效算法。

若一個問題多輸入僅限定於整數，而求解該問題多算法A的計算時間不超過其輸入長度和其中整數的最大絕對值的一個多項式，則稱A為偽多項式時間算法，比如，背包問題和劃分問題，則可以認為它是理論上相對容易求解的困難問題。