最小支撐樹

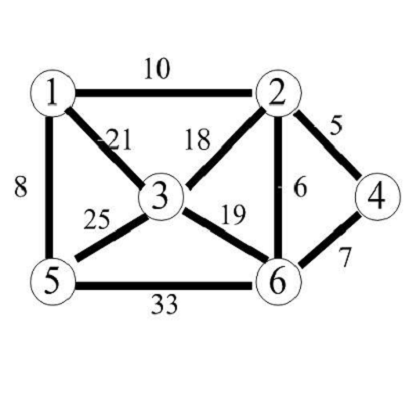
設G=（V，E）是一個無向連通網，生成樹上各邊的權值之和為該生成樹的代價，在G的所有生成樹中，代價最小的生成樹就稱為最小支撐樹，或稱最小生成樹。

基本介紹

• 中文名：最小支撐樹
• 外文名：Minimal spanning tree
• 所屬：：計算機科學

物種介紹

生成樹

由圖遍歷的過程中經過的邊加上圖的所有頂點所構成的子圖。

生成樹的特點

（1）n個頂點的連通子圖的生成樹是一個極小連通子圖，它包含圖中所有頂點和n-1條邊（但有n-1條邊的圖不一定是生成樹）。

（2）生成樹中任意兩個頂點間的路徑是唯一的。

樹的權

生成樹T各邊的權值總和稱為該樹的權。

最小生成樹

將權最小的生成樹稱為圖的最小生成樹。

Krusal和Prim算法是兩個構造最小生成樹的著名算法。

普里姆算法

設為 N=(V,E,C)連通網，TE是N的最小支撐樹的邊的集合。

① 算法開始時， U= {u o }(u o ∈ V), TE= ○ ；

② 找到滿足

weight(u,v)=min{weight(u 1 ,v 1 )| u 1 ∈ U, v 1 ∈ V-U }, 的邊，把它併入集合

TE中，v同時併入U。

③ 反覆執行② ,直至 V=U 時終止算法。

吉林大學網路教材

吉林大學教材

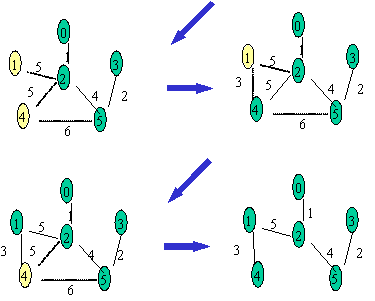
吉林大學教材

普里姆算法執行過程示例

由上述圖解算法的過程知，構造的最小生成樹不一定唯一，但最小生成樹的權值之和一定是相同的。