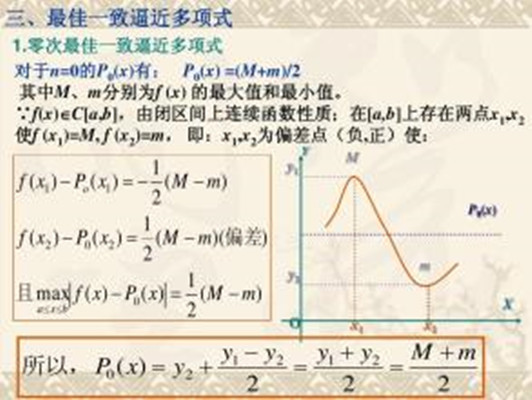
設 f(x) ∈C[a,b],若存在P*n屬於Hn,使得△(f,P*n)=En,則稱P*n是f(x)在[a,b]上的最佳一致逼近多項式。最佳一致逼近多項式是一種用多項式去逼近函式的方法,通常可利用切比雪夫定理進行求解。
基本介紹
- 中文名:最佳一致逼近多項式
- 外文名:polynomials of best uni-form approximation
- 學科:數學
- 求解方法:切比雪夫定理
- 性質:存在性;唯一性
- 領域:數值分析
基本概念,偏差,最小偏差,偏差點,交錯點組,多項式,多項式,例題,
基本概念
偏差
若 ,
, ,則稱
,則稱 為
為 與
與 在[a,b]上的偏差。
在[a,b]上的偏差。





註: ,
, 的全體組成一個集合,記作:
的全體組成一個集合,記作: ,它有下界0。
,它有下界0。



最小偏差
若記集合 的下確界為:
的下確界為:





偏差點
設 ,
, ,若在
,若在 上有
上有 ,則稱
,則稱 是
是 的偏差點。
的偏差點。






若 ,則稱
,則稱 是“正”的偏差點。
是“正”的偏差點。


若 ,則稱
,則稱 是“負”的偏差點。
是“負”的偏差點。


註:由 在
在 上的連續性可知,偏差點一定存在。
上的連續性可知,偏差點一定存在。


交錯點組
若函式 在其定義域的某一區間
在其定義域的某一區間 上存在 n 個點
上存在 n 個點 ,使得:
,使得:





則稱點集 為函式
為函式 在區間
在區間 上的一個交錯點組,點
上的一個交錯點組,點 為交錯點。
為交錯點。




多項式
假定 ,若存在
,若存在 使
使 則稱
則稱 是
是 在
在 上的最佳一致逼近多項式或最小偏差逼近多項式。
上的最佳一致逼近多項式或最小偏差逼近多項式。






定理1:若 ,則總存在
,則總存在 ,使得
,使得



定理2:設 是區間
是區間 上的連續函式,
上的連續函式, 是
是 的
的 次最佳一致逼近多項式,則
次最佳一致逼近多項式,則 必須同時存在正負偏差點。
必須同時存在正負偏差點。






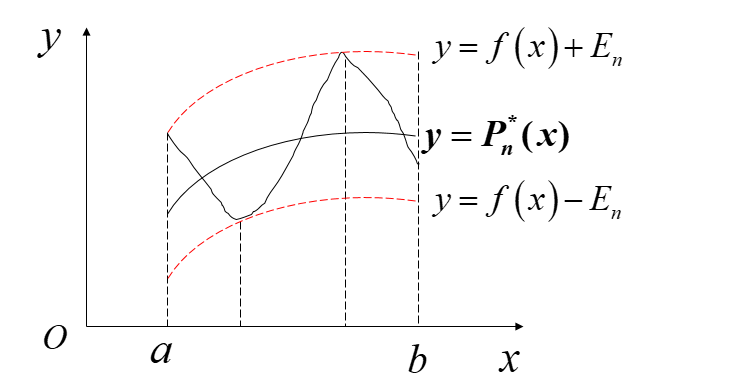
推論1:如果 ,則在
,則在 中存在唯一的最佳一致逼近多項式
中存在唯一的最佳一致逼近多項式


推論2:如果 ,則其最佳一致逼近多項式
,則其最佳一致逼近多項式 就是
就是 的一個拉格朗日插值多項式。
的一個拉格朗日插值多項式。



多項式
設 ,
, 在
在 內不變號,
內不變號, 是
是 的一次最佳一致逼近多項式,則a,b屬於交錯點組。
的一次最佳一致逼近多項式,則a,b屬於交錯點組。





由定理可知:
至少存在3個交錯點,



因為 是
是 的一次最佳一致逼近多項式 ,所以
的一次最佳一致逼近多項式 ,所以



因為 ,所以
,所以 單調,所以
單調,所以 在
在 只有一個零點,記作
只有一個零點,記作 ,即
,即






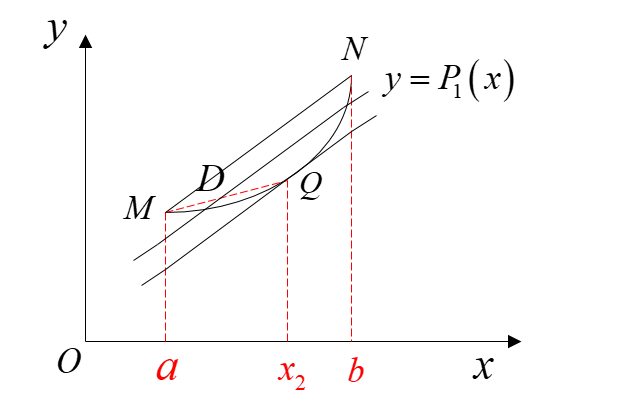
則有:



幾何意義如下圖:
例題
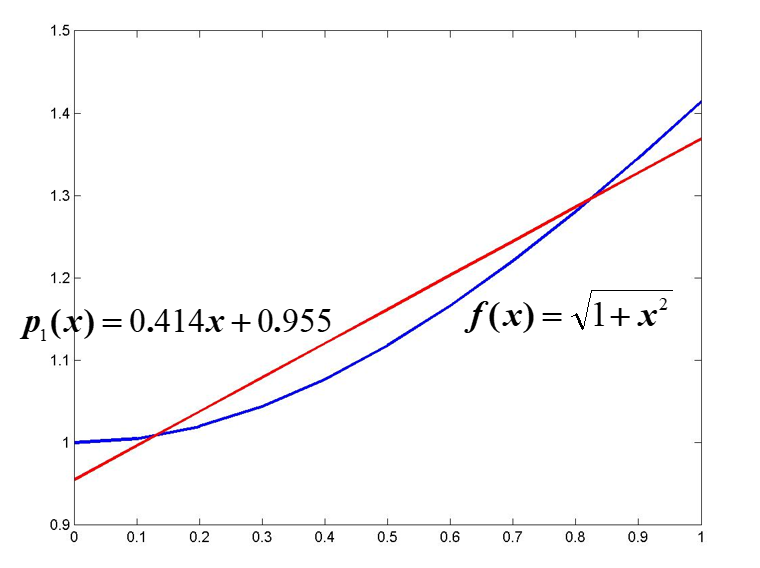
求函式 在區間
在區間 上的最佳一致逼近多項式。
上的最佳一致逼近多項式。


解:


由


得:

即:

解得: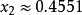
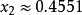
故

所求一次最佳逼近多項式為

故

誤差限為: