曲線束,是經典代數幾何的常用術語。所有曲線束的曲線都通過它的兩條基線的交點。所有曲線束的公共點(基線的交點)叫做曲線束的中心。
基本介紹
- 中文名:曲線束
- 外文名:Pencil
- 類別:數學名詞
- 映射:Φ:X→P^n.
定義,定理,曲線束的中心,
定義
當給出了線性獨立函式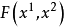 及
及 與及不同的參數值λ ,方程式
與及不同的參數值λ ,方程式
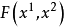


在各種參數值λ 的條件下,曲線 的集合構成一族曲線,它叫做曲線束。
的集合構成一族曲線,它叫做曲線束。

曲線 及
及 組成線束的基線,第一曲線屬於參數值 λ=0 的曲線束。我們亦把第二曲線歸入曲線束中,它是當參數 λ 無限增大時的結果。
組成線束的基線,第一曲線屬於參數值 λ=0 的曲線束。我們亦把第二曲線歸入曲線束中,它是當參數 λ 無限增大時的結果。


為了使第二基線不是曲線束的例外情況,最方便地時以下列的比來代替參數λ



定理
所有曲線束的曲線都通過它的兩條基線的交點。
實際上,基線的交點坐標使函式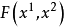 及
及 為零。因而帶著任意的係數 λ 的它們的和也等於零,即是當參數 λ 未任意值時,方程式
為零。因而帶著任意的係數 λ 的它們的和也等於零,即是當參數 λ 未任意值時,方程式 都成立。
都成立。
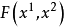


這意味著,曲線當每一交點坐標都滿足曲線束的任何曲線方程式,而這些交點本身式屬於曲線束中所有曲線的。
曲線束的中心
所有曲線束的公共點(基線的交點)叫做曲線束的中心。
通過平面上非曲線束中心的任何一點,有一而且只有一條曲線束的曲線。
設 是平面上任意一點,但不是曲線束的中心。現在要證明,有一而且只有一條曲線束的曲線通過它。
是平面上任意一點,但不是曲線束的中心。現在要證明,有一而且只有一條曲線束的曲線通過它。

以值 代入曲線束 (4') 的方程式,得
代入曲線束 (4') 的方程式,得


如果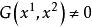 ,即是點 M* 不在第二基線 (5) 上,那么,由方程式 (a) 可以得到比值
,即是點 M* 不在第二基線 (5) 上,那么,由方程式 (a) 可以得到比值 ,即
,即
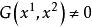


如果  及
及  ,那么方程式 (a) 給出了 p=0。即是第二基線通過 M 點。
,那么方程式 (a) 給出了 p=0。即是第二基線通過 M 點。


如果  及
及  ,那么方程式 (a) 變為恆等式,p 及 q 為不定。在這種情況下坐標
,那么方程式 (a) 變為恆等式,p 及 q 為不定。在這種情況下坐標 滿足基線 (5) 點兩個方程式。而 M* 與曲線束的中心重合,這是與定理假設的條件矛盾的。
滿足基線 (5) 點兩個方程式。而 M* 與曲線束的中心重合,這是與定理假設的條件矛盾的。




