1932年,Wigner在量子力學中引進了時間反演,乍一看來,這是與空間反演相似的一個分立對稱性,實際上不然。這是用詞不當。嚴格地說,所謂的時間反演對稱乃是指運動的可逆性,即把一個過程用攝像機拍下來,然後把膠捲倒過來放映,假如看上去運動規律(當然不是指“現象”)與順放時一樣,就叫做“時間反演守恆”。
基本介紹
- 中文名:時間反演算符
- 外文名:Time reversal operator
- 定義:運動的可逆性
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:時間反演對稱性
概念
基本原理
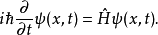
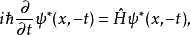
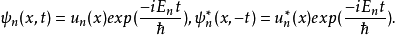
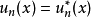
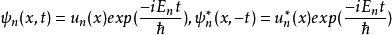
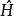
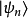
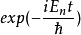
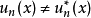
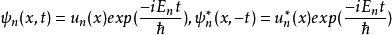
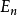
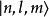
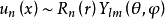
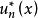
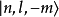
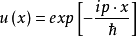
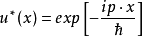

1932年,Wigner在量子力學中引進了時間反演,乍一看來,這是與空間反演相似的一個分立對稱性,實際上不然。這是用詞不當。嚴格地說,所謂的時間反演對稱乃是指運動的可逆性,即把一個過程用攝像機拍下來,然後把膠捲倒過來放映,假如看上去運動規律(當然不是指“現象”)與順放時一樣,就叫做“時間反演守恆”。
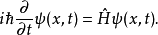
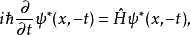
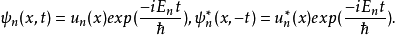
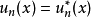
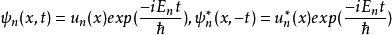
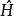
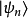
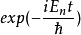
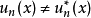
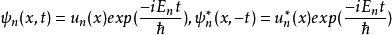
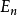
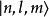
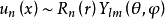
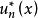
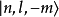
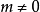
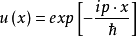
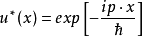
1932年,Wigner在量子力學中引進了時間反演,乍一看來,這是與空間反演相似的一個分立對稱性,實際上不然。這是用詞不當。嚴格地說,所謂的時間反演對稱乃是指運動的...
時間反演(time reversal )是指空間坐標保持不變,時間坐標改變符號的變換。...... 式中T為時間反演算符。此變換下動量為k及自旋為r的粒子變成動量為-k、自旋為-...
時間反演T(time reversal T)是指空間坐標保持不變,時間坐標改變符號的變換。...... 式中T為時間反演算符。這是典型的分立變換。此變換下動量為k及自旋為r的粒子...
時間反演對稱性又叫做時間反轉不變性。時間反演對稱性描述的是在時間反演操作下:物理系統的對稱性。雖然在一些限定條件下存在時間反演對稱性,但是由於熱力學第二定律...
[第17講] 時間反演不變性、演化可逆性及能譜下確界 ——兼及Dirac符號是“有...——取決於算符的指數! [第20講] 量子理論內在邏輯自洽性分析 ——又一個常...
§ 3.8 空間反演和宇稱3.8 A 量子態和算符的宇稱3.8 B 宇稱守恆定律3.8 C 宇稱不守恆的發現§ 3.9 時間反演對稱性3.9 A 時間反演算符...
A3.1時間反演態與時間反演算符 A3.2角動量本徵態的時間反演性質 A3.3時間反演不變數與時間反演對稱系統 A3.4人態和出態的時間反演態 主要參考書 參考文獻[...
