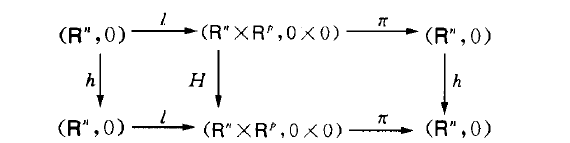
映射芽接觸等價(contact equivalence ofmap-germs)奇點理論的一個概念.它是反映兩個映射的零點集局部拓撲等價的概念。
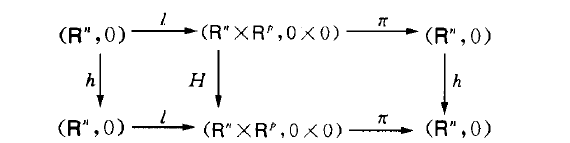
映射芽接觸等價(contact equivalence ofmap-germs)奇點理論的一個概念.它是反映兩個映射的零點集局部拓撲等價的概念。設.f,g:(R^,o)-(Rp,O)是兩個可微映射芽，若存在C一微分同胚芽...
映射芽的接觸等價是奇點理論的一個概念，它是反映兩個映射的零點集局部拓撲等價的概念.設 是兩個可微映射芽，若存在C微分同胚芽 和可微映射芽 ，這裡GL(R)是一般線性群，，I為R上的恆等變換，使得 ，則稱f和g是C接觸等價的。若φ與L均為Cr可微映射芽，則稱f與g是C接觸等價的，當φ與L僅為連續時，就稱...
映射芽左等價(left equivalence of map-germs)兩個映射之間的一種關係.指兩個映射僅經過其值域的坐標變換後便可以把一個變為另一個·設f,g: (R",0)}(R",0)是兩個可微映射芽，若存在C0'微分同胚芽k;(R0,0)}(R",0)使得概述圖所示是交換的，即g=k 0 f，則稱f與g是左等價的.若k是C'微分同胚芽...
映射芽右等價是兩個映射之間的一種關係.指兩個映射只經過其定義域的坐標變換後便可以把一個變為另一個。映射芽右等價(right equivalence of map-germs)兩個映射之間的一種關係.指兩個映射只經過其定義域的坐標變換後便可以把一個變為另一個.設f,g:(R0，0)(R"，0)是兩個可微映射芽，若存在C微分同胚芽h...
精確定義如下:設f記群少y和交於的定義參見“映射芽的右等價”，“映射芽的左等價”，“映射芽的右一左等價”和“映射芽的接觸等價f，稱f相對於群·了是k決定的，若對任意g任了，只要x-y=0，都有f的酬軌道包含g，即映射芽f與g相對於夕等價.若k=，則稱f是無限決定的.對於一個映射f，若存在一個正...
映射芽右-左等價(right-left equivalence ofmap-germs)兩個映射之間的一種關係.指兩個映射經過其定義域及值域的坐標變換後可以把一個變為另一個.設f,g: (R0,0>}(R0,0>是兩個可微映射芽。映射芽右-左等價(right-left equivalence ofmap-germs)兩個映射之間的一種關係.指兩個映射經過其定義域及值域的坐標...
映射芽決定性是一個數學術語。映射芽決定性，反映映射在一點的局部性質，它可以由其在該點的某些導數所決定.設N,P為光滑流形，EP,CN表示由無窮次可微函式芽（N，x）R的全體構成的集合，y0表示y。的局部坐標，p=dime.設M為的R線性子空間.給定一個無窮次可微映射芽f:（N，x）（P,y），若存在可微映射芽g;...
映射芽接觸等價(contact equivalence ofmap-germs)奇點理論的一個概念.它是反映兩個映射的零點集局部拓撲等價的概念。設.f,g:(R^,o)-(Rp,O)是兩個可微映射芽，若存在C一微分同胚芽}p: (R", 0) } (R", 0)和可微映射芽L: (R", 0)GL(Rp)，這裡GL(Rp)是一般線性群，L(0)=I,I為R”上的恆等...
3 關於穩定性和唯一性研究 證明了相對映射芽及其相對開折在左右等價下的穩定性和無窮小穩定性是等價的；建立了相對映射芽開折的一種與相對映射芽左右等價相容的等價關係，得到了同一軌道中相對映射芽的通用開折在這種等價意義下是唯一的；給出了相對映射芽開折穩定的一個充分必要條件。
