整閉包是域論中代數閉包的推廣。設 A 是一個環,R 是 A 的一個子環。令 C 是 A 的所有在 R 上整的元素組成的集合,則可以證明,C 是 A 的一個包含 R 的子環,稱之為 R 在 A 中的整閉包。
基本介紹
- 中文名:整閉包
- 外文名:integral closure
- 適用範圍:數理科學
整相關,整性質,
整相關
[integrally dependent]
設 A 是一個環,R 是 A 的一個子環。對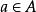 ,如果存在 R 上的一個首項係數為 1 的多項式使得 a 是它的一個根,即存在
,如果存在 R 上的一個首項係數為 1 的多項式使得 a 是它的一個根,即存在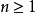 ,
,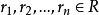 使得
使得
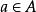
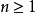
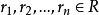
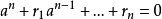
令 C 是 A 的所有在 R 上整的元素組成的集合,則可以證明,C 是 A 的一個包含 R 的子環,稱之為 R 在 A 中的整閉包。如果C=R,則稱 R 在 A 中是整閉的(integrally closed)。
環的整相關是域的代數擴張概念的推廣。
整性質
任意交換的帶單位元的環 R 的元素 a 稱為整數環 Z 上的整元,簡稱整元。如果 a 是一個首一的整係數多項式的零點,R的所有整元構成一個帶單位元的子環。複數域 C 中的 Z 上的整元就是所謂的代數整數。 所有的代數整數構成一個整環 稱為代數整數環。
整性質在有限群表示論中起重要作用。 設 G 為有限群,g=|G|為群 G的階,G在複數域 C 上的群代數 C[G] 的中心 Z(C[G]) 是 C 上的交換代數。 令 b1,b2,...,bn是 G 的所有共扼類的類和, 則它們構成Z(C[G])的一個基底 而且易知它們都是整元,因而它們的代數整數組合都是整元。

