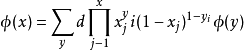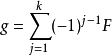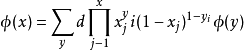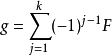故障樹分析是一種描述事故因果關係的有方向的"樹",是系統安全工程中的重要的分析方法之一,他能對各種系統的危險性進行識別評價,既適用於定性分析,又能進行定量分析,具有簡明,形象化的特點,體現了以系統工程方法研究安全問題的系統性,準確性和預測性。
基本介紹
- 中文名：故障樹分析
- 外文名：fault tree analysis
- 提出年代：1961年
基本釋義,故障事件及表示符號,故障數的編制與化簡,故障樹定性分析,故障樹定量分析,故障樹分析的基本程式,
基本釋義
故障樹分析是一種邏輯演繹的分析工具，用描繪事故發生的有向邏輯樹，分析事故的現象、原因及結果，從而找出預防事故的措施。它是一種複雜系統可靠性分析方法。
1961年美國貝爾電話研究所的沃森(watson)在研究民兵式飛彈發射控制系統的安全性時首先提出了這種方法。隨後，該研究所的門斯(A.B.Mearns)等人改進了這種方法，成功地預測了飛彈發射意外事故。波音公司進一步發展了故障樹分析技術，使之與計算機的運用相結合。在美國原子能委員會進行的核電站危險性評價中，大量地用故障樹分析方法進行機率危險性評價，1974年發表了WASH-1400研究報告，引起世界各國關注，並被迅速推廣到各工業部門的安全工作中。
故障事件及表示符號
故障樹是演繹地表示事故或故障事件發生原因及其邏輯關係的邏輯樹圖。故障樹的形狀象一株倒置的樹，其中的事件一般都是故障事件。
事件及事件符號故障樹用來表示事件間的因果關係及邏輯關係。在故障樹的每個分支中，上層故障事件是下一層故障事件的結果，下層事件是引起上一層故障事件的原因。事件間的邏輯關係用邏輯門表示。因此，把作為結果的上層事件稱作邏輯門的輸出事件，而把作為原因的下層事件稱作輸入事件。
位於故障樹最上部的事件叫做頂事件，一般為造成嚴重後果的故障事件或事故，是故障樹分析、研究的對象。位於故障樹各分支末端的事件叫做基本事件，它們是造成頂事件發生的最初始的原因。在系統安全分析中，故障樹的基本事件主要是物的故障及人的失誤。位於故障樹頂事件與基本事件之間的諸事件被稱為中間事件，它們是造成頂事件發生的原因，又是基本事件造成的結果。
故障樹的各種事件的內容記在事件符號之內。常用的事件符號有如下幾種。
矩形符號。表示需要進一步分析的故障事件，如頂事件和中間事件。
圓形符號。表示作為基本事件的故障事件。
房形符號。表示作為基本事件的正常事件。有時，系統元素的正常狀態對於上一層故障事件的發生是必不可少的，但是正常事件並非分析研究和採取措施的對象，故用特殊記號區別於其他故障事件。
菱形符號。表示當前不能進一步分析或認為沒有進一步分析必要的省略事件。在故障樹分析中，菱形符號內的事件按基本事件對待。
橢圓形符號。是一種條件事件符號。條件事件是指輸入事件發生能夠導致輸出事件發生;輸入事件不發生。橢圓形符號要與限制門結合使用。
邏輯門及其符號故障樹的鄰近兩層事件之間用邏輯門相連線。對於任一上層故障事件，作為其發生原因的下層事件可能有兩個或兩個以上，即對應於每個輸出事件有多個輸入事件。輸出事件和輸入事件之間的邏輯關係有邏輯與、邏輯或及邏輯非等。
邏輯“與門”表示全部輸入事件都發生則輸出事件才發生，只要有一個輸入事件不發生則輸出事件就不發生的邏輯關係。
邏輯“或門”表示只要有一個或一個以上輸入事件發生則輸出事件就發生，只有全部事件都不發生，輸出事件才不發生的邏輯關係。有時把“與門”記為“AND門”，“或門”記為“OR門”。
異或門不能同時發生輸入事件中任一個發生而其他都不發生的時候，輸出事件發生。在故障樹中，除了上述幾種邏輯門外，還有一種叫做限制門的邏輯門，它與條件事件符號相結合，表示只有滿足一定條件的輸入事件發生時，輸出事件才發生，如果該條件未被滿足，則輸出事件不會發生的邏輯關係。
當故障樹比較複雜時，用轉移符號可省去與其他部分內容相同的部分，或把故障樹的一部分畫在另外的地方，使故障樹變得簡明、清晰。表示由其他部分引入的為轉入符號;表示向其他部分轉出的是轉出符號。輸入符號及轉出符號應有相互一致的編號。
故障數的編制與化簡
故障樹的編制是故障樹分析的第一步，也是以後分析的基礎。首先要確定作為分析研究對象的頂事件。一般把後果嚴重的或發生頻繁的系統故障事件或事故作為頂事件。然後分析直接造成頂事件發生的原因事件，並用恰當的邏輯門與頂事件連線。再找出造成直接原因事件發生的原因事件，確定恰當的邏輯門與直接原因事件連線。如此逐層分析，直到畫出基本事件為止。
正確地編制故障樹，需要深刻地了解系統及其結構，元素、子系統的故障模式及影響，以及有關係統安全的豐富知識。系統元素有以下三種故障。
(1)原生故障。由於元素自身缺陷或老化等原因引起的故障，不同元素的原生故障往往是統計獨立的。
(2)次生故障。由於元素之外的一些原因引起的故障，不同元素的次生故障可能是統計不獨立的，即由共同原因引起的。
(3)指令故障。到達元素的指令故障，往往是由系統內其它元素故障引起的。
利用電子計算機自動編制故障樹，已經進行了長期的研究。鑒於實際系統的複雜性及故障模式的多樣性，當前只能編制非常簡單系統的故障樹。
故障樹布爾表達式故障樹事件之間的關係是邏輯關係，這些邏輯關係只能藉助布爾代數來描述。用布爾代數建立的故障樹數學模型叫做故障樹布爾表達式，它是進行故障樹分析，特別是定量分析的基礎。
布爾代數又稱邏輯代數，它的運算是邏輯運算，變數為二值變數，僅取0或1中的一個值。布爾代數中的函式為二值函式，其數值也只能取0或1中的一個，它通過布爾代數變數的邏輯運算組合而成。布爾代數中的邏輯運算主要有邏輯積運算及邏輯和運算，邏輯運算規則與普通代數運算規則有很大不同。
在故障樹分析中，研究的事件是取故障發生或不發生兩種狀態之一的事件，不考慮任何中間狀態。於是，可以利用布爾代數作數學工具來研究。故障樹中故障事件發生的狀態對應於布爾代數值1，故障事件不發生時對應於數值0;邏輯“與門”對應於布爾代數的邏輯積運算，邏輯“或門”對應於邏輯和運算。如果用二值變數表示故障樹中各事件的狀態，則很容易用這些二值變數的邏輯運算組合來表達故障樹事件之間的關係。這就是故障樹的布爾表達式。可以由頂事件開始，自上而下用邏輯運算取代邏輯門來逐層展開，最後獲得布爾表達式。如果輸入事件為E1，E2，…，En，輸出事件為E，邏輯與門的布爾代數式為
邏輯或門的布爾代數式為
E=E1∪E2∪…∪En
當故障樹中同樣的基本事件出現在兩處以上的地方時，應考慮是否有多餘的基本事件。利用布爾代數的運算規則可以去除多餘的基本事件。這一過程被稱作故障樹的化簡。
故障樹定性分析
故障樹定性分析包括三方面的內容。
(1)查明造成系統故障或事故的全部初始原因，以便針對初始原因採取改進措施。
(2)找出最容易引起系統故障或事故發生的初始原因集合。
(3)考察哪些初始原因對系統故障或事故發生影響更大。
通過編制故障樹，獲得了引起頂事件發生的全部初始原因。接下去的分析是找出基本事件的最小割集合與最小徑集合，比較基本事件的重要度。
最小割集合與最小徑集合故障樹中的全部基本事件都發生，則頂事件一定發生。但大多數情況下並不一定全部基本事件都發生頂事件才發生，而是只要某些基本事件組合在一起發生就可以導致頂事件發生。在故障樹分析中，把能使頂事件發生的基本事件的集合叫做割集合。換言之，割集合中的基本事件發生，則頂事件必然發生。在割集合中，能夠引起頂事件發生的最小限度的基本事件集合，即其中有一個基本事件不發生，頂事件就不發生的割集合叫做最小割集合。最小割集合表明系統故障或事故發生的途徑。
故障樹中的全部基本事件都不發生，則頂事件一定不發生。但是某些基本事件的組合不發生，也可以使頂事件不發生。能保證頂事件不發生的基本事件的集合叫做徑集合。在徑集合中，保證頂事件不發生的最小限度的基本事件集合，即其中若有一個基本事件發生就會導致頂事件發生的徑集合叫做最小徑集合。最小徑集合表明應該如何採取措施使一些初始原因不同時出現就可以避免事故。
最小割集合求法比較流行的是利用布爾表達式和福賽爾(J.B.Fussell)法。
(1)利用布爾表達式。基本作法是把布爾表達式展開成事件邏輯積或邏輯和的形式，實行邏輯和運算的各項就為割集合，利用布爾代數法則化簡後，得到最小割集合。
(2)福賽爾法。又稱行列法，是一種適合計算機運算的求解最小割集的方法。特別適用於求複雜故障樹的最小割集合。該方法的基本出發點是，邏輯“與門”使割集合內包含的基本事件數增加;邏輯“或門”使割集合的數目增加。具體做法是：自上而下用輸入事件取代輸出事件。如果遇到邏輯“與門”，則把輸入事件寫在同一行里;如果遇到邏輯“或門”，則把輸入事件分別寫在不同行里。這樣一直進行到全部中間事件被基本事件取代為止，每一行里的基本事件構成一個割集合。比較這些割集合，消去不是最小的割集合，就得到了所求的最小割集合。
最小徑集合求法首先把故障樹變換為與之對偶的成功樹，然後求該成功樹的最小割集合，則成功樹的最小割集合就是原故障樹的最小徑集合。把故障樹的故障發生事件用與其相反的故障不發生事件代替，把邏輯“與門”用邏輯“或門”、邏輯“或門”用邏輯“與門”代替，得到的新樹就是成功樹。
基本事件的結構重要度造成系統故障或事故的初始原因很多，但它們所起的作用是不同的。在採取對策時，應該按輕重緩急，優先解決那些最重要的問題。基本事件在故障樹結構中所處的位置決定了它們對頂事件影響的重要程度，即基本事件的結構重要度。基本事件結構重要度是說明基本事件重要程度相對順序的定性評價指標，只有相對意義。
根據各基本事件在最小割集合中出現的情況，可以判斷其結構重要度順序：在包含較少基本事件的最小割集合中出現的基本事件結構重要度較高;在不同最小割集合中出現次數較多的基本事件結構重要度較高。
故障樹定量分析
故障樹定量分析根據各基本事件發生機率求解頂事件發生機率，從而為機率危險性評價提供依據。對於簡單的故障樹，根據機率論中事件邏輯積與事件邏輯和的機率計算公式，把故障樹布爾表達式轉變為由基本事件發生機率計算頂事件發生機率的公式。代入基本事件發生機率後，即可算出頂事件發生機率。對於複雜的故障樹，人力解算費時費力，往往利用計算機求解。故障樹定量分析涉及一些特殊的理論和方法。
相關結構理論由巴洛(R.E.Barlow)和普魯森(F.Proschan)提出的複雜系統可靠性分析理論，是故障樹分析的數學基礎。
(1)相關結構。如果故障樹中任一基本事件的發生與否都影響頂事件的發生，則稱該故障樹為相關結構。前述的利用布爾代數法則化簡後的故障樹是相關結構。事件狀態仍然為二值的，只能取0或1中的一個值。具有相關結構的故障樹，其頂事件的狀態完全取決於基本事件的狀態，即頂事件狀態是基本事件狀態的函式。該函式的形式取決於故障樹的結構，故稱相關結構函式。包含幾個基本事件的故障樹，其相關結構函式被稱作n階相關結構函式。n階相關結構函式的一般形式為
(2)頂事件發生機率的精確解。對於不十分複雜的故障樹，可以精確地求解頂事件發生機率。對相關結構函式表達式兩端取數學期望，則頂事件發生機率可表示為
式中Sj為前j個最小徑集合中包含的基本事件不發生機率的乘積，或者按下式計算：
式中Fj為前j個最小割集合中基本事件發生機率的乘積。
(3)頂事件發生機率的近似解。當故障樹非常複雜時，精確求解頂事件發生機率是很困難的。為了節省計算機記憶體及運算時間，可以求近似解。利用最小徑集合或最小割集合的計算公式計算前n項，就可以得到相當精度的近似解。
當故障樹中的基本事件統計不獨立時，只能計算頂事件發生機率的上、下限。它的上限為發生機率最小的最小徑集合發生機率;它的下限為發生機率最大的最小割集合的發生機率。
(4)基本事件的重要度。在相關結構理論中，把對應於割集合的二值矢量叫做割矢量，對於某基本事件，如果它發生則頂事件發生，否則頂事件也不發生的割矢量為該基本事件的臨界割矢量。顯然，臨界割矢量數目多的基本事件對頂事件發生的影響較大。對於n階相關結構，調查除某基本事件外的2個二值矢量中臨界割矢量比例，就得到了該基本事件的結構重要度。除結構重要度之外，還有機率重要度、關鍵重要度等評價指標。
蒙特卡羅法利用數學模擬機率過程及隨機數來確定一事件能否發生及發生機率的方法。它可以解決僅依靠經驗、分析等方法難以解決的問題。在故障樹的基本事件非常多的情況下，前面介紹的分析方法的套用受到了限制，可以藉助蒙特卡羅法解決。在套用蒙特卡羅法進行故障樹分析時，把各種事件，事件間的邏輯關係及事件發生的機率分布輸入到計算機中，計算機產生隨機數並判斷事件能否發生，按規定時間內基本事件發生情況來確定頂事件的發生機率。
故障樹分析的基本程式
故障樹分析的基本程式如下:
1.熟悉系統
要詳細了解系統狀態及各種參數,繪出工藝流程圖或布置圖.
2.調查事故
收集事故案例,進行事故統計,構想給定系統可能要發生的事故.
3.確定頂上事件
要分析的對象時間即為頂上事件,對調查的事故進行全面分析,找出後果嚴重且較易發生的事故做為頂上事件.
4.確定目標值
5.調查原因事件
6.畫出故障樹
從頂上事件起,一級一級找出直接原因事件,到所要分析的深度,按其邏輯關係,畫出故障樹.
7.定性分析
8.確定事件發生機率
9.比較
10.分析
