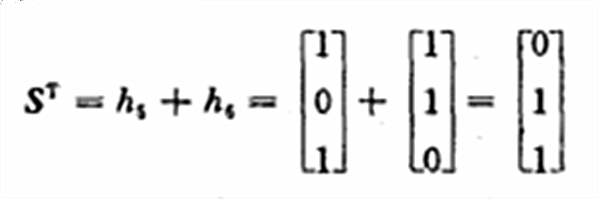定義
(n,k)分組碼都是糾正單個錯誤的。假設出現兩位錯,且錯誤模式為
和
,則錯誤伴隨式是H的第i列和第j列相應位按模2求和的結果。因為H的各列互不相同,故
,所以有錯。但是,它可能與第k列相同,即
。這時,也就是說,如果錯了兩位,不僅不能正確解碼,而且也發現不了錯誤,這是人們不希望的。
例如(7,4)碼的校驗矩陣為
若第5位和第6位有錯,則伴隨式為
它恰好與第3列相同。這時,就將錯誤模式0000110誤認為0010000,於是,就將實際無錯的第3位錯糾了。
所以,上述由H矩陣構成的碼,只能糾正單個錯誤,而不能發現兩個錯誤,當然更談不上糾正兩個錯誤了。為了能糾正一個錯誤,又能夠發現兩個錯誤,可以在糾單錯碼的基礎上加以擴展,使構造的H矩陣保證任意3列線性無關。
構造長度為q的q進制里德-索羅門碼,這樣的碼叫做擴展碼。該碼可糾正t=(n-k)/2個符號錯誤,且既可以將它看做是對可以糾正t一1個錯誤、檢測t個錯誤(擴展)的碼添加一個
奇偶校驗,還可以將它看做是對可以糾正t個錯誤的碼加上一個額外的信息符號。
擴展碼不是循環碼,但是可以用頻域技術對其進行編碼和解碼。這種碼的特性相對來說易於理解,解碼方法的邏輯是其屬性的有效證明。
分類
單拓展碼
示例:要想構造可糾正一個錯誤、檢測兩個錯誤的長度為7、GF(8)上的里德一索羅門碼,我們可以使用
,信息
進行系統編碼後,成為
。位置3的傅立葉變換為
。
現在,我們在位置7和位置5上生成兩個錯誤,接收序列就變成
。序列
。的校正子多項式是
。
位置4的校正子是0。嘗試糾正單個錯誤,則產生連線多項式
,且位置2的校正子分量得到了正確的預測。因此,位置7上的符號就不再需要了。錯誤值就是
的值,即
,所以收到的(7,4)碼的碼字可以被糾正成
,前4個符號是信息。
另外,我們也可以在位置5和位置3上製造兩個錯誤,那么接收到的序列就是
,
的校正子多項式是
。
位置3的值是
。糾正單個錯誤的連線多項式是
,但是它不能正確地預測下一個勻量。所以我們假設邊緣頻率
是正確的,並將它加到計算出的
上去,得到糾正兩個錯誤的碼的校正子
。雙錯誤糾正的關鍵方程為:
,
。
消去
,得到
,
。它的根是
和
,表明錯誤在位置5和位置3上。
雙拓展碼
示例:我們考慮GF(8)_E的(9,5)里德一索羅門碼的情形。在這個例子中,我們有一個由5個符號組成的信息序列
。將第一個和最後一個符號作為邊緣符號對待,在頻域中將它們分別置於位置3和位置0。這樣,我們便從糾正單個錯誤的里德一索羅門碼的頻譜開始:
。反向變換將給出(7,5)里德一索羅門碼的碼字:
。
現在將兩個額外的信息符號加到碼字的兩端,構成(9,5)里德一索羅門碼字
下面假設在位置8和位置5上產生了錯誤,這樣便產生接收序列
向下的3階項並沒有作為校正子析出,而附加的符號則加到了合適的點上,得到
。校正子中的各項會隨著階數的增加而增
的倍數,表明出現了單個錯誤,且關鍵方程的解為
。因此,錯誤序列的譜就是
。
解碼得到了正確的實現,且所有的信息都可以直接從c(z)中得到。