接觸問題

彈性力學中研究的兩接觸物體受壓力後產生局部應力和變形的問題的統稱。軸承、凸輪機構、齒輪、硬度計、軋鋼機的軋輥、橋樑支座和剛性壓頭等在使用中都有接觸問題。接觸問題曾是套用數學力學家面臨的一大難題。在過去一百多年的研究中，產生了一系列有效的數學方法。

基本介紹

  • 中文名：接觸問題
  • 外文名：Contact problem
  • 屬於：彈性力學
  • 類型：物理
  • 人物：H.R.赫茲
正文,

正文

材料在接觸區的變形受到各個方面的限制，因而處於三向應力狀態。接觸應力具有明顯的局部性質，而且總是隨著離開接觸區距離的增大而迅速衰減。一般在接觸表面中心的壓應力最大。
德國的H.R.赫茲於1881年用數學彈性力學方法導出了接觸問題的一個公式。他隨後所作的實驗表明，理論計算值與實測值相差不到1%。在推導公式中他作了如下假設：①接觸區應力不超過彈性極限（見材料的力學性能）；②接觸面尺寸和物體接觸點的曲率半徑相比甚小，可將接觸點附近物體近似地看作是二次拋物面；③沿接觸面分布的壓力垂直於接觸面。
如果不考慮出現在接觸體之間的摩擦力，接觸問題就可大為簡化。在計算機械零件所遇到的接觸問題中,有很多場合可略去摩擦力。在互相接觸的零件之間加一層油膜，摩擦力就可明顯下降；如果一個零件對另一零件運動的速度不太大，則可忽略流體的動力效應。
解決接觸問題所依據的基本關係如下：①變形方面，原為點接觸的物體，受力後接觸表面為橢圓形（一般情況）或圓形（特殊情況，例如兩個球接觸）；原為線接觸的物體，受力後接觸表面為矩形。此外，兩接觸物體的變形符合變形連續條件。②物理方面，材料處於彈性階段，且接觸表面上的壓應力和接觸物體的應變呈線性關係。③靜力平衡方面，根據接觸表面壓應力分布規律求得的合力應等於外載荷。
根據上述基本關係可推導出各種接觸問題的公式，最一般的情況為兩個物體作點接觸。設R1，R1’為物體1在接觸點的兩個主曲率半徑；R2，R2’為物體2在接觸點的兩個主曲率半徑；φ為R1、R2兩曲率半徑所在平面間的夾角；P為外載荷。在這種情況下，接觸面為橢圓，其半長軸為：
接觸問題
在橢圓中心處的壓應力q0為最大值，即
接觸問題
接觸面上的壓力分布為：
接觸問題
兩物體中心移動距離δ為：
接觸問題
以上各式中E1和v1分別為物體1的彈性模量和泊松比；E2和v2分別為物體2的彈性模量和泊松比，參量A為：
接觸問題
x、y分別為沿接觸橢圓的長軸和短軸的坐標；α、β、λ為係數，在引進
接觸問題
後，它們的值可以根據算出的θ值由下表查出：
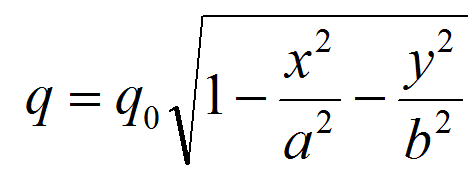
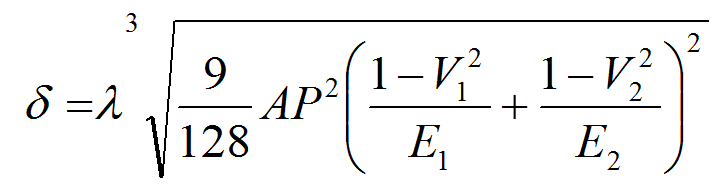
θ
0
10
20
30
35
40
45
50
α
6.612
3.778
2.731
2.379
2.136
1.926
1.754
β
0
0.319
0.408
0.493
0.530
0.576
0.604
0.641
λ
-
0.851
1.220
1.453
1.550
1.637
1.709
1.772
θ
55
60
65
70
75
80
85
90
α
1.611
1.486
1.378
1.284
1.202
1.128
1.061
1.000
β
0.678
0.717
0.759
0.802
0.846
0.893
0.944
1.000
λ
1.828
1.875
1.912
1.944
1.967
1.985
1.996
2.000
接觸應力同載荷呈非線性關係是接觸應力的重要特徵之一,計算表明,最大接觸壓應力同載荷的立方根（或平方根）成正比，這是因為隨著載荷的增加，接觸面積也增大，其結果使接觸面上的最大壓應力的增長比載荷的增長慢。接觸應力的另一特徵是應力與材料的彈性模量和泊松比有關，這是因為接觸面積的大小與接觸物體的彈性變形有關。
影響接觸應力的因素很多，其中主要的有：①殘餘應力（由於接觸點附近應力很大，有時會進入塑性狀態而引起殘餘應力）；②熱應力（兩接觸面相對滑動時摩擦會引起熱應力）；③潤滑，它影響熱應力及切向載荷，還可能產生動壓油膜而影響接觸應力的大小及分布；④接觸面的幾何形狀偏差等。
在靜載荷或緩慢移動載荷作用下，材料的接觸強度（即抵抗接觸載荷的能力）取決於表層材料的塑性變形。載荷緩慢移動要比完全靜止更為有利，這是因為載荷完全靜止不動時，會在較軟的物體上壓出凹坑，而緩慢移動只使較軟的物體表面產生均勻的塑性變形，因而一般不改變物體的巨觀幾何形狀。
目前，在解決彈性體接觸問題方面已採用有限元法，通過它可計算各種形狀、材料和載荷下的接觸問題，並且所得的結果精度較高。系統研究接觸問題，還須用複變函數和積分變換等數學工具。

相關詞條

熱門詞條

聯絡我們