掛谷問題

掛谷問題，由日本數學家掛谷宗一(かけや そういち Soichi Kakeya，1886-1947)於1917年提出，又稱“掛谷轉針問題”(Kakeya needle problem)。這個問題的數學表述為：長度為1的線段在平面上做剛體移動（轉動和平移），轉過180度並回到原位置，掃過的最小面積是多少？

基本介紹

• 中文名：掛谷問題
• 外文名：The problem of hanging grain
• 提出者：掛谷宗一
• 提出時間：1917年
• 適用領域：數學

問題原型

一位武士在上廁所時遭到敵人襲擊，矢石如雨，而他只有一根短棒，為了擋住射擊，需要將短棒旋轉一周360°（支點可以變化）。但廁所很小，應當籃歸烏屑使短棒掃過的面積儘可能小。面積可以小到多少？

問題提出

由日本數學家掛谷宗一(かけや そういち Soichi Kakeya，1886-1947)於1917年提出，又稱“掛谷轉針問題”(Kakeya needle problem)。這個問題的數學表述為：長度為1的線段在平面上做剛體移動（轉動和平移），轉過180度並回到原位置，掃過的最小面積是多少？精槳棗

其中轉過180°和轉過360°是實質等同的，因此只考慮旋轉180°的情況。

這個問題引起當時很多人的興趣，如1925年伯考夫(G. D. Birkhoff，1884-1944)在他寫的《相對論的來源、性質與影響 The origin, nature, and influence of relativity》一書中提到：“近幾年日本數學家掛谷宗一提出的問題，是同樣令人感興趣的問題。”

解決歷程

定義長度為 1 的線段可在點集中轉過180°，那這樣的點集被稱為掛谷集(Kakeya Set)或別西科維奇集(Besicovitch set)。這樣就把掛谷問題轉化為了求面積最小的掛谷集。

掛谷問題中短棒有多種旋轉方式，主要有：半圓、圓、三角、環以及內擺線等。

半圓

首先，我們考慮繞著線段一端轉半圈的情形。毫無疑付槓才樂問地，這圖形是個半徑為1的半圓，面積是π/2≈1.57079633。

顯然，這是很差的一種設計。如果把定點放線上段中點，則是稍好一點，面積為π/4≈0.785398163。

圓

數學家們肯定不會考慮上述這些幾乎沒有技術含量的東西。在掛谷宗一提出這個問題後，有數學家發現，若這個線段在正三角形（高為 1，邊長為 2/√3 ）中每一頂點處都旋轉 60°，可以算出這種情況下，線段掃過面積為 1/√3。

三角形

當然，若線段夾在兩個圓之間，轉過180°的面積既小於整個圓環，又大於半個圓環，當內圓的半徑無限增大時，面積趨近於π/8，但始終不等於π/8。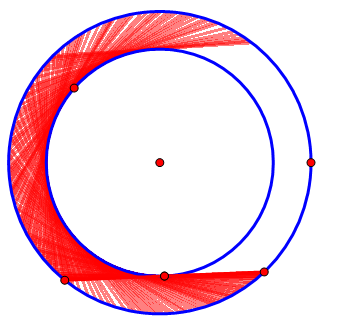

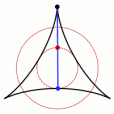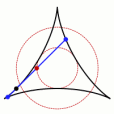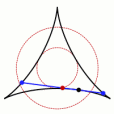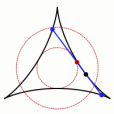
圓環

能否讓掃過的面積剛好為π/8呢，掛谷宗一本人想到的是藉助三尖內擺線盼探，計算表明，這種情況下線段掃過的面積是 π/8 。掛谷本人及其他許多數學家都認為這就是最小面積了。

內擺線

問題解決

1928年，蘇聯數學家別西科維奇（Besicovitch，Abram Samoilovitch，1891-1970）解決了這個問題，答案是可以任意小。

1920 年前蘇聯數學家貝西科維奇（A．S．Besicovitch）在自己的研究領域提出一個類似的問題:是否存在一個面積（若爾當測度）為 0 的平麵點集，它在每一方向上都有長度1的線度？ 1928 年別西科維奇解決了自己的問題，即構造出面積任意小的平麵點集(貝西科維奇集)，在每一方向上都有長度 1 的線段。

佩龍樹

貝西科維奇用了一種構造性的證明方法。想像一個高為1的等邊三角形，把它平分，再把兩個直角三角形稍微疊在一起，如圖《佩龍樹》。這個新圖形面積比三角形小，但是在其中，屬於 [-120°,-60°] 的每個角都能找出邊長 ≥1 的線段。

重新開始，把三角形平均分為 8 個，把它們兩兩疊在一起，再兩兩疊在一起，這種圖形就叫做“佩龍Perron樹”。如果我們重複這個步驟，把三角形分為 16 個、32 個、……、 2^n個，顯然整個圖形的面積可以越來越小，並且可以證明圖形面積無限趨近於0。

把 3 個佩龍樹分別旋轉 0°，120°，240° 併疊在一起，可以看到，最後的圖形在每個角上都有邊長 ≥1 的線段，這也就是說它是一個貝西科維奇集，並且面積任意小。

事實上，這是一個和掛谷集問題類似的問題。貝西科維奇本人將這兩個問題稱為姜艱愚孿生問題。匈牙利數學家鮑爾（Pál）曾經證明了能夠把一條單位長線段連續地從一條直線移動到另一翻蘭凝條直線，並且掃過的面積任意小。藉助這個鮑爾的貢獻，貝西科維奇剛才構造的貝西科維奇集化為我們想要的掛谷集，成功地解決了掛谷問題。最後的結果如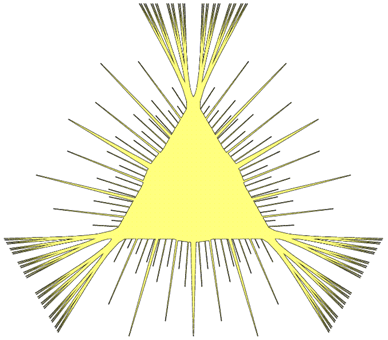圖1。

圖1

他的結論出乎絕大多數人的意料：短棒掃過的面積可以任意地小（因而沒有最小值）。在德國數學家佩龍在 1928 年和另一位數學家舍恩伯格在 1962 年兩度化簡後，這個問題成為了數學中的經典例子。

解答完善

雖然別西科維奇轎祝臘給出了解答，但是這並不完美，因為如此構造出的掛谷集不是單聯通的（他們得到的掛谷集有很多洞）。1965 年沃克（R. J. Walker）首先找到比掛谷本人解答的面積更小的單連通域掛谷集。同年布洛姆、舍恩伯格和坎寧安（F.Cunningham）先後造出面積為 （5 - 2√2）π/24 的單連通掛谷集。這個面積被命名為 Bloom-Schoenberg number。 1971 年坎寧安終於在單位圓內作出面積可以任意小的單連通掛谷集，完全解決了單連通性和有界性兩方面的問題。同時，他證明了如果限於星形（即圖形記憶體在一點，連線它與圖形中任一點的線段整個在圖形中），則掛谷集的面積不小於 π/108。

在此之後，掛谷問題又有了多種形式的推廣，比如 1971 年戴維斯（R.O.Davies）證明了一條半徑為 1 的圓弧轉過，掃過的面積不能任意小。此外，將線段改為寬度很小的長方形這類問題也開始有人研究。

貝西科維奇用了一種構造性的證明方法。想像一個高為1的等邊三角形，把它平分，再把兩個直角三角形稍微疊在一起，如圖《佩龍樹》。這個新圖形面積比三角形小，但是在其中，屬於 [-120°,-60°] 的每個角都能找出邊長 ≥1 的線段。

重新開始，把三角形平均分為 8 個，把它們兩兩疊在一起，再兩兩疊在一起，這種圖形就叫做“佩龍Perron樹”。如果我們重複這個步驟，把三角形分為 16 個、32 個、……、 2^n個，顯然整個圖形的面積可以越來越小，並且可以證明圖形面積無限趨近於0。

把 3 個佩龍樹分別旋轉 0°，120°，240° 併疊在一起，可以看到，最後的圖形在每個角上都有邊長 ≥1 的線段，這也就是說它是一個貝西科維奇集，並且面積任意小。

事實上，這是一個和掛谷集問題類似的問題。貝西科維奇本人將這兩個問題稱為孿生問題。匈牙利數學家鮑爾（Pál）曾經證明了能夠把一條單位長線段連續地從一條直線移動到另一條直線，並且掃過的面積任意小。藉助這個鮑爾的貢獻，貝西科維奇剛才構造的貝西科維奇集化為我們想要的掛谷集，成功地解決了掛谷問題。最後的結果如圖1。

圖1

他的結論出乎絕大多數人的意料：短棒掃過的面積可以任意地小（因而沒有最小值）。在德國數學家佩龍在 1928 年和另一位數學家舍恩伯格在 1962 年兩度化簡後，這個問題成為了數學中的經典例子。

解答完善

雖然別西科維奇給出了解答，但是這並不完美，因為如此構造出的掛谷集不是單聯通的（他們得到的掛谷集有很多洞）。1965 年沃克（R. J. Walker）首先找到比掛谷本人解答的面積更小的單連通域掛谷集。同年布洛姆、舍恩伯格和坎寧安（F.Cunningham）先後造出面積為 （5 - 2√2）π/24 的單連通掛谷集。這個面積被命名為 Bloom-Schoenberg number。 1971 年坎寧安終於在單位圓內作出面積可以任意小的單連通掛谷集，完全解決了單連通性和有界性兩方面的問題。同時，他證明了如果限於星形（即圖形記憶體在一點，連線它與圖形中任一點的線段整個在圖形中），則掛谷集的面積不小於 π/108。

在此之後，掛谷問題又有了多種形式的推廣，比如 1971 年戴維斯（R.O.Davies）證明了一條半徑為 1 的圓弧轉過，掃過的面積不能任意小。此外，將線段改為寬度很小的長方形這類問題也開始有人研究。