拋物發展系統(parabolic evolution system) 一類重要的線性發展方程。
基本介紹
- 中文名:拋物發展系統
- 外文名:parabolic evolution system
一個巴拿赫空間X中的線性發展方程
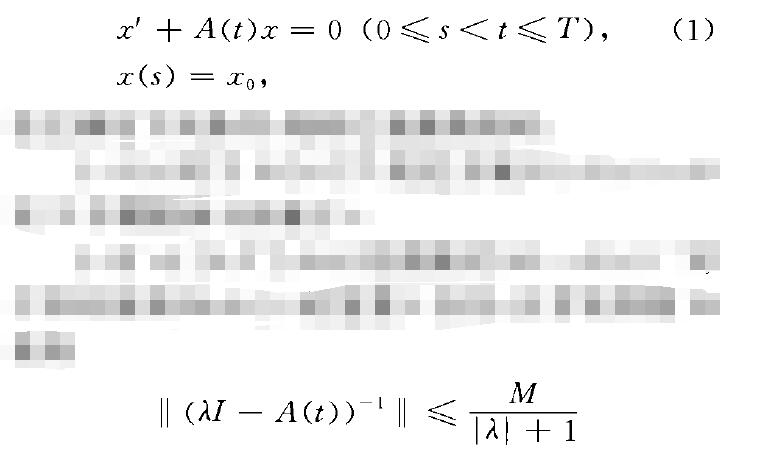
拋物發展系統
若它滿足下列條件,則稱它是拋物型的: 1.A(t)對於0毛t毛T的定義域D(A(t))=D 在X中稠密和不依賴於t. 2.對tE [O,T],A(t)的預解式(.11-A(t))一’對於所有使得Re .}鎮0的複數幾存在,且存在常數M 使得
對tE [0,T〕成立. 3.存在常數L和。G a鎮1,使得日(A (t)一 A(s))A(r)一‘11鎮Llt一、I0,對、,t,=E Co,T〕成立. 設(1>是拋物型的,則存在0鎮、鎮t鎮T上的惟一的發展系統U(t,s)具有以下性質: 1.}{U(t,s) }} }C,對於O}s}t}7'成立,這裡 C是正常數. 2.對於0毛sGt毛7',U(t,s):X}D和U(t,s)對,強可微且景U(t,s)EL(X,X),}f O}sGtG7'強連續,此外 GT成立.

拋物發展系統
3.{}反丁曰(t,s) 日dl s)和}} A(t)U(t,s)A一’(、) 成立.
毛C對於0毛sGt毛T 4.對每一0鎮sGT和xoEX,(1)有惟一解二((t) 一U(t,s)xo. 5.若f (t)在[s,T〕上是赫爾德連續的,則對每一xo E X,柯西問題
有惟一古典解
